Функция Кантора

Гребенка Кантора

Назовём Канторовой гребёнкой множество D на плоскости Oxy, состоящее из всех точек ,координаты которых удовлетворяют следующим условиям: 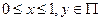, где 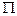- множество Кантора на оси Oy. Канторова гребёнка является совершенным нигде не плотным множеством на плоскости. Множество D состоит из всех точек исходного единичного квадрата, абсциссы которых произвольны 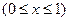, а ординаты могут быть записаны в виде троичной дроби, не содержащей единицы среди своих троичных знаков.

Можно ли множества B (кладбище Серпинского) и D (гребёнка Кантора) выразить через множество Кантора 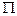с помощью действий дополнения до отрезка [0, 1] и декартова произведения? Очевидно, что множества B и D выражаются элементарно:

B = x

D = [0, 1] x

Можно ли отобразить непрерывно некоторое нигде не плотное на сегменте [0,1] множество на сам этот отрезок?

Да, возьмём нигде не плотноe множество Кантора. На первом шаге построения положим в точках смежного интервала первого рода значение функции равное 0,5. На втором шаге каждому смежному интервалу второго рода положим значение функции соответственно 0.25 и 0.75. Т.е. мы как бы делим каждый отрезок на оси Oy пополам (y_i) и ставим в соответствующем смежном интервале значение функции равное значению yi.

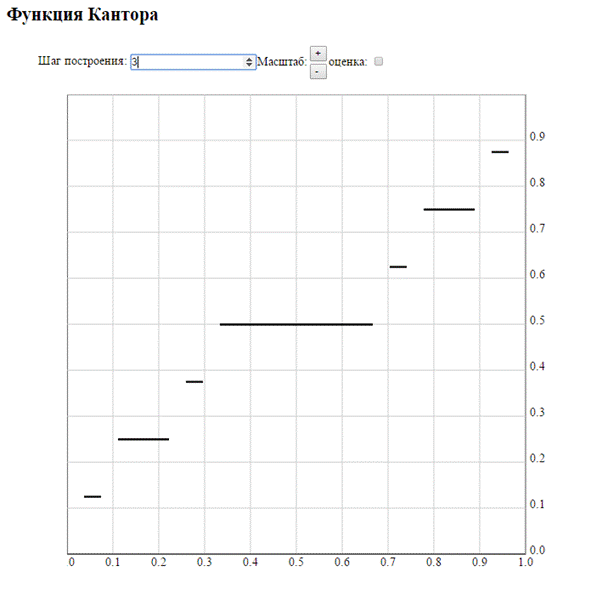
В результате мы получили неубывающую функцию (было доказано в рамках курса «Избранные главы математического анализа»), определённую на отрезке [0, 1] и постоянную в некоторой окрестности каждой точки из множества [0, 1]\ 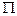. Построенная функция называется функцией Кантора (канторова функция), а её график, приведённый ниже - ''чёртовой лестницей''.

Обратите внимание на фрактальную структуру функции:

Функция удовлетворяет следующему неравенству:

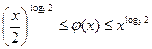
Функция Кантора является непрерывной на отрезке [0, 1]. Она не убывает на [0, 1] и множество её значений составляет весь отрезок [0, 1]. Поэтому, функция не имеет скачков. А т.к. монотонная функция не может иметь других точек разрыва, кроме скачков (см. критерий непрерывности монотонных функций), то она является непрерывной.

Любопытным является наблюдение, что график непрерывной функции кантора невозможно нарисовать ''не отрывая карандаша от бумаги''.

Дата добавления: 2015-06-27