Всюду непрерывная, но нигде не дифференцируемая функция

Построим вспомогательную функцию 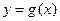на отрезке [0, 1] по шагам. На нулевом шаге зададим две точк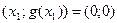и:

и .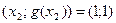

Далее зафиксируем параметр 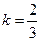. На первом и последующем шагах будем задавать точки по следующему правилу: для каждых двух соседних по оси абсцисс ранее построенных точек 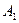и 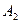мы будем строить две новые точк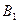и и 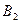центрально-симметрично относительно центра прямоугольника, задаваемого точкам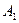и и 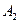с коэффициентом k. То есть, на первом шаге задаются две новые точк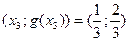и:

и 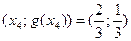, и т.д.

На (m+1)- ом шаге в дополнении к ранее построенным точкам с абсциссами

,

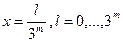строятся по две точки во всех промежутках по оси абсцисс между соседними уже построенными точками. Это построение выполняется так: промежутки по оси абсцисс между соседними точками (прямоугольники со сторонами a и b) делятся на 3 равные части каждый. Затем две новые точки строятся по одной из нижеприведённых схем:

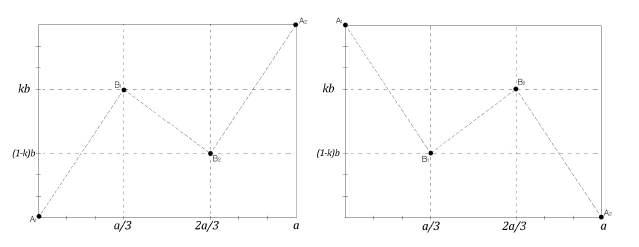
В зависимости от того, какая из соседних точек 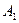или 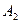выше, используем левую или правую схему. На первом шаге, как это было показано выше, принимаем a = b = 1.

Повторяем построение счётное число раз при m = 1, 2, 3, …. В результате нами будет получен фрактал, который будет подобен, с точностью до некоторого аффинного преобразования (растяжение, сжатие, поворот) любой своей части, заключенной в каждой полосе:

;

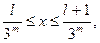
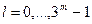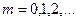
В результате построения фрактала получим функцию 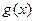, определённую на множестве точек

, ; (*)

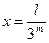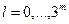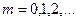которое всюду плотно на отрезке [0, 1].

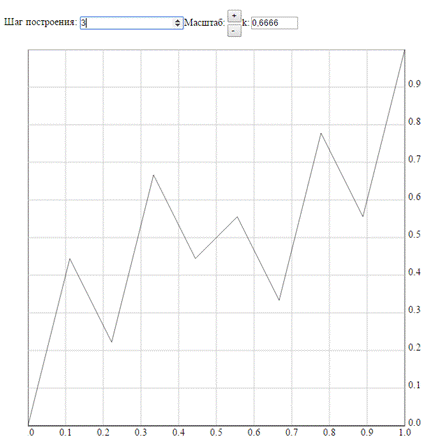
Какими свойствами обладает построенная функция?

· в каждой точке вида (*) либо строгий максимум, либо строгий минимум, т.е. функция g(x) нигде не монотонная, и имеет плотные на сегменте [0, 1] множества точек строгих экстремумов;

· функция g(x) непрерывна, и даже равномерно непрерывна на множестве точек (*);

· построенная непрерывная на сегменте [0, 1] функция не имеет ни в одной точке данного отрезка даже односторонних производных;

Вышеуказанные свойства были доказаны в рамках курса «Избранные главы математического анализа».

В рассмотренном примере мы полагали параметр 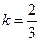. Изменяя значение данного параметра, можно получить семейства функций со своими особыми свойствами.

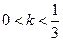· . Эти функции непрерывны и строго монотонно возрастающие. Имеют нулевые и бесконечные производные (соответственно, точки перегиба) на множествах точек, всюду плотных на сегменте [0, 1].

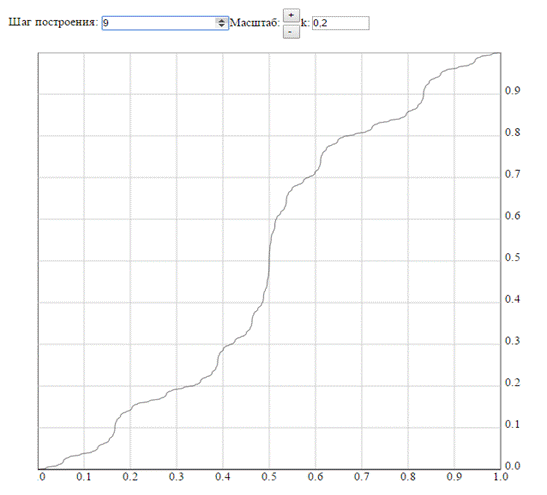
· . Получена линейная функция y = x

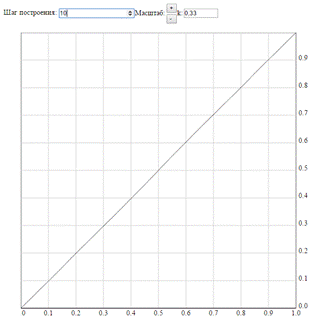
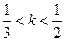· . Свойства семейства функций те же, что и при значениях к из первого диапазона .

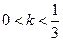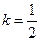· . Нами получена функция Кантора, которая была подробно изучена нами ранее.

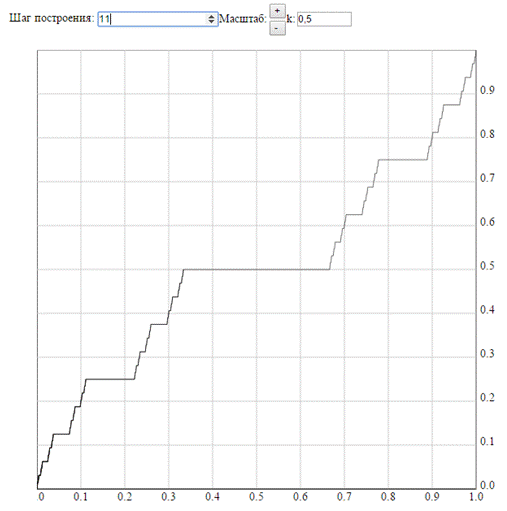
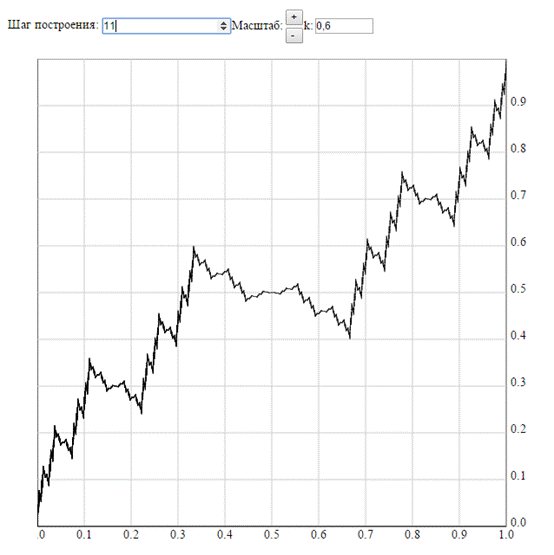
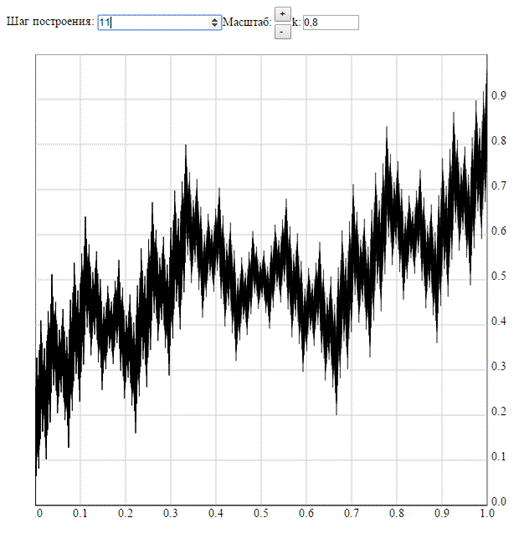
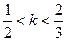· . Данные функции непрерывны, нигде не монотонны, имеют строгие минимумы и максимумы, нулевые и бесконечные (обоих знаков) односторонние производные на множествах точек, всюду плотных на сегменте [0, 1].

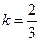· . Данная функция была изучена нами выше.

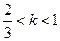· . Функции из этого диапазона обладают теми же свойствами, что и функция при .

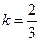Заключение.

В своей работе я реализовала некоторые примеры из курса «Избранные главы математического анализа». В данную работу были вставлены скриншоты визуализированных мною программ. На деле они все интерактивные, студент может посмотреть вид функции на конкретном шаге, строить их сам итерационно и приближать масштаб. Алгоритмы построения, а также некоторые функции библиотеки Skeleton были специально подобраны и усовершенствованы под данный тип задач (рассматривались в основном фракталы).

Данный материал, несомненно будет полезен преподавателям и учащимся и является хорошим сопровождением лекций курса «Избранные главы математического анализа». Интерактивность данных визуализаций помогает лучше понять природу построенных множеств и облегчают процесс восприятия материала учащимися.

Описанные программы вошли в библиотеку визуальных модулей проекта www.visualmath.ru, например, вот уже рассмотренная нами функция Кантора:

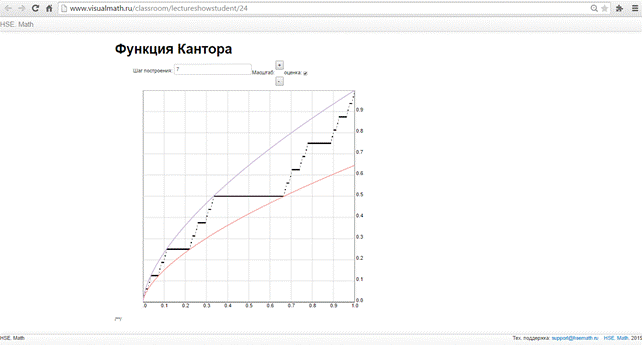
В дальнейшем предполагается расширять список визуализируемых задач и улучшать алгоритмы построения для более эффективной работы программ. Работа в проекте www.visualmath.ru, несомненно принесла много пользы и опыта, навыки работы в команде, умение оценивать и максимально понятно преподносить учебный материал.

Литература.

1. Б. Гелбаум, Дж Олмстед, Контрпримеры в анализе. М.: Мир.1967.

2. Б.М. Макаров и др. Избранные задачи по вещественному анализу. Невский диалект, 2004.

3. Б.Мандельброт. Фрактальная геометрия природы. Институт компьютерных исследований, 2002.

4. Ю.С. Очан, Сборник задач и теорем по ТФДП. М.: Просвещение. 1963.

5. В.М. Шибинский Примеры и контрпримеры в курсе математического анализа. М.: Высшая школа, 2007.

6. Р.М.Кроновер, Фракталы и хаос в динамических системах, М.:Постмаркет, 2000.

7. А. А. Никитин, Избранные главы математического анализа // Сборник статей молодых ученых факультета ВМК МГУ, 2011 / ред. С. А. Ложкин. М.: Издательский отдел факультета ВМК МГУ им. М.В. Ломоносова, 2011. С. 71-73.

8. Р.М.Кроновер, Фракталы и хаос в динамических системах, М.:Постмаркет, 2000.

9. Фрактал и построение всюду непрерывной, но нигде недифференцируемой функции // XVI международные Ломоносовские чтения: Сборник научных трудов. – Архангельск: Поморский госуниверситет, 2004. С.266-273.

[1] Объединение счетного числа открытых множеств (смежных интервалов) открыто, а дополнение открытому множеству – замкнуто.

[2] 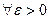любой окрестности 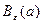точки а множества Кантора, найдется хотя бы одна точка из 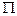, отличная от а.

[3] Замкнуто и не содержит изолированных точек (каждая точка является предельной).

[4] Существует не более чем счетное множество 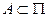, всюду плотное в .

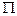[5] Множество A – нигде не плотно в пространстве R, если любое открытое множество этого пространства содержит другое открытое множество, целиком свободное от точек множества A.

[6] Точка 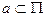, в любой окрестности которой содержится несчетное множество точек данного множества.

[7] Будем говорить, что множество на плоскости нигде не плотно в метрическом пространстве R, если любой открытый круг этого пространства содержит другой открытый круг, целиком свободный от точек данного множества.

Дата добавления: 2015-06-27