Разбор цепочек

Примеры грамматик и языков.

Замечание: если при описании грамматики указаны только правила вывода Р, то будем считать, что большие латинские буквы обозначают нетерминальные символы, S - цель грамматики, все остальные символы - терминальные.

1) Язык типа 0: L = {a² | n ³ 1}

G(L): S ® aaCFD

F ® AFB | AB

AB ® bBA

Ab ® bA

AD ® D

Cb ® bC

CB ® C

bCD ® e

2) Язык типа 2: L={цепочки из 0 и 1 с одинаковым числом 0 и 1}

G(L): S ® ASB | AB

AB ® BA

A ® 0

B ® 1

3) Язык типа 2: L = {(ac)ⁿ (cb)ⁿ | n > 0}

G(L): S ® aQb | accb

Q ® cSc

4) Язык типа 3: L = {w ^ | w Î {a,b}⁺, где нет двух рядом стоящих а}

G(L): S ® A^ | B^

A ® a | Ba

B ® b | Bb | Ab

Цепочка принадлежит языку, порождаемому грамматикой, только в том случае, если существует ее вывод из цели этой грамматики. Процесс построения такого вывода (а, следовательно, и определения принадлежности цепочки языку) называется разбором.

С практической точки зрения наибольший интерес представляет разбор по контекстно-свободным (КС и УКС) грамматикам. Их порождающей мощности достаточно для описания большей части синтаксической структуры языков программирования, для различных подклассов КС-грамматик имеются хорошо разработанные практически приемлемые способы решения задачи разбора.

Рассмотрим основные понятия и определения, связанные с разбором по КС-грамматике.

Определение: вывод цепочки b Î (VT)^* из S Î VN в КС-грамматике G = (VT, VN, P, S), называется левым (левосторонним), если в этом выводе каждая очередная сентенциальная форма получается из предыдущей заменой самого левого нетерминала.

Определение: вывод цепочки b Î (VT)^* из S Î VN в КС-грамматике G = (VT, VN, P, S), называется правым (правосторонним), если в этом выводе каждая очередная сентенциальная форма получается из предыдущей заменой самого правого нетерминала.

В грамматике для одной и той же цепочки может быть несколько выводов, эквивалентных в том смысле, что в них в одних и тех же местах применяются одни и те же правила вывода, но в различном порядке.

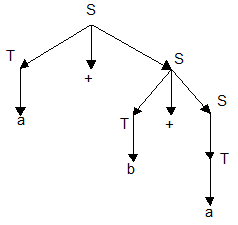
Например, для цепочки a+b+a в грамматике

G = ({a,b}, {S,T}, {S ® T | T+S; T ® a|b}, S)

можно построить выводы:

(1) S®T+S®T+T+S®T+T+T®a+T+T®a+b+T®a+b+a

(2) S®T+S®a+S®a+T+S®a+b+S®a+b+T®a+b+a

(3) S®T+S®T+T+S®T+T+T®T+T+a®T+b+a®a+b+a

Здесь (2) - левосторонний вывод, (3) - правосторонний, а (1) не является ни левосторонним, ни правосторонним, но все эти выводы являются эквивалентными в указанном выше смысле.

Для КС-грамматик можно ввести удобное графическое представление вывода, называемое деревом вывода, причем для всех эквивалентных выводов деревья вывода совпадают.

Определение: дерево называется деревом вывода ( или деревом разбора) в КС-грамматике G = {VT, VN, P, S), если выполнены следующие условия:

(1) каждая вершина дерева помечена символом из множества (VN È VT È e), при этом корень дерева помечен символом S; листья - символами из (VT È e);

(2) если вершина дерева помечена символом A Î VN, а ее непосредственные потомки - символами a₁, a₂,..., a_n, где каждое a_i Î (VT È VN), то A ® a₁a₂...a_n - правило вывода в этой грамматике;

(3) если вершина дерева помечена символом A Î VN, а ее единственный непосредственный потомок помечен символом e, то A ® e - правило вывода в этой грамматике.

Пример дерева вывода для цепочки a+b+a в грамматике G:

Определение: КС-грамматика G называется неоднозначной, если существует хотя бы одна цепочка a Î L(G), для которой может быть построено два или более различных деревьев вывода.

Это утверждение эквивалентно тому, что цепочка a имеет два или более разных левосторонних (или правосторонних) выводов.

Определение: в противном случае грамматика называется однозначной.

Определение: язык, порождаемый грамматикой, называется неоднозначным, если он не может быть порожден никакой однозначной грамматикой.

Пример неоднозначной грамматики:

G = ({if, then, else, a, b}, {S}, P, S),

где P = {S ® if b then S else S | if b then S | a}.

В этой грамматике для цепочки if b then if b then a else a можно построить два дерева вывода.

Однако это не означает, что язык L(G) обязательно неоднозначный. Определенная нами неоднозначность - это свойство грамматики, а не языка, т.е. для некоторых неоднозначных грамматик существуют эквивалентные им однозначные грамматики. Если грамматика используется для определения языка программирования, то она должна быть однозначной. В приведенном выше примере разные деревья вывода предполагают соответствие else разным then. Если договориться, что else должно соответствовать ближайшему к нему then, и подправить грамматику G, то неоднозначность будет устранена:

S ® if b then S | if b then S’ else S | a

S’ ® if b then S’ else S’ | a

Проблема, порождает ли данная КС-грамматика однозначный язык (т.е. существует ли эквивалентная ей однозначная грамматика), является алгоритмически неразрешимой.

Однако можно указать некоторые виды правил вывода, которые приводят к неоднозначности:

(1) A ® AA | a

(2) A ® AaA | b

(3) A ® aA | Ab | g

(4) A ® aA | aAbA | g

Пример неоднозначного КС-языка:

L = {aⁱ b^j c^k | i = j или j = k}.

Интуитивно это объясняется тем, что цепочки с i=j должны порождаться группой правил вывода, отличных от правил, порождающих цепочки с j=k. Но тогда, по крайней мере, некоторые из цепочек с i=j=k будут порождаться обеими группами правил и, следовательно, будут иметь по два разных дерева вывода. Доказательство того, что КС-язык L неоднозначный, приведен в [3, стр. 235-236]. Одна из грамматик, порождающих L, такова:

S ® AB | DC

A ® aA | e

B ® bBc | e

C ® cC | e

D ® aDb | e

Очевидно, что она неоднозначна.

Дерево вывода можно строить нисходящим либо восходящим способом.

При нисходящем разборе дерево вывода формируется от корня к листьям; на каждом шаге для вершины, помеченной нетерминальным символом, пытаются найти такое правило вывода, чтобы имеющиеся в нем терминальные символы “проектировались” на символы исходной цепочки.

Метод восходящего разбора заключается в том, что исходную цепочку пытаются “свернуть” к начальному символу S; на каждом шаге ищут подцепочку, которая совпадает с правой частью какого-либо правила вывода; если такая подцепочка находится, то она заменяется нетерминалом из левой части этого правила.

Если грамматика однозначная, то при любом способе построения будет получено одно и то же дерево разбора.

Дата добавления: 2015-06-27