Лекция 14

Контрольные вопросы и задание

Выводы по 6-ой главе

Оценка продукционных систем:

Достоинства:

1. Высокая степень детализации знаний.

2. Независимость отдельных элементов знаний друг от друга.

3. Рассмотрение базы знаний как совокупности активных процессов допускает асинхронную организацию решения задач с высокой степенью параллельности.

4. Продукционные модели применимы к области со слабоформализированными знаниями (медицина, биология и т.д.).

Недостатки:

1. Продукционные базы знаний не наглядны.

2. Низкая эффективность стратегии управления.

6.6.1.. Охарактеризуйте продукционную модель представления знаний. Приведите примеры представления знаний правилами. В чем отличия между продукционными системами с прямыми, обратными и двунаправленными выводами?

6.6.2. Опишите функционирование механизма вывода продукционной ЭС и охарактеризуйте его составляющие: компоненту вывода и управляющую компоненту.
6.6.3. Сформулируйте собственные примеры прямого и обратного вывода в ЭС продукционного типа.

6.6.4. Разработайте программную реализацию интеллектуальной системы с продукционным представлением знаний и механизмом вывода на базе правила Modus Ponendo Ponens.

6.6.5. Выполните формализацию знаний средствами продукционной модели, которые могут использоваться в интеллектуальной системе для поддержки задач диагностики экономического и финансового состояния предприятия (других задач).

6.6.6. Выполните представление знаний средствами описанных моделей для известной Вам игры.

Глава 7. Представление и вывод неопределённых знаний в системах искусственного интеллекта

7.1. Представление и вывод при нечётких знаниях.

Известно, что количественные данные (знания) могут быть неточными, при этом существуют количественные оценки такой неточности (доверительный интервал, уровень значимости, степень адекватности и т.д.). Лингвистические знания также могут быть неточными. Для учета неточности лингвистических знаний используется теория нечетких множеств, предложенная Л. Заде в 1965 г. Этому ученому принадлежат слова: «фактически нечеткость может быть ключом к пониманию способности человека справляться с задачами, которые слишком сложны для решения на ЭВМ». Развитие исследований в области нечеткой математики привело к появлению нечеткой логики и нечетких выводов, которые выполняются с использованием знаний, представленных нечеткими множествами, нечеткими отношениями, нечеткими соответствиями и т. д.

7.1.1. Определение нечёткого множества.

Нечеткие множества выражаются понятиями: «сильно», «очень», «слабый», «несколько» и т.п.

1 2 3 4 5 6 7 8 9 10

Нет ничего: 0; Не много: 5 – 8;

Очень мало: 1 -2; Много: 9 – 10;

Мало: 1- 4; Очень много: >10.

Нечеткое подмножество А множества элементов U области рассуждений определяется функцией принадлежности µА отраженной на интервале [0;1], которая связывает с каждым элементом y є U число µА(у) в интервале [0;1], которая представляет собой степень принадлежности у к А.

Элемент подмножества А называется синглетон.

Нечеткое множество А можно рассмотреть как объединение синглетонов, которые можно коротко описать:

А = µА(у)/у – при бесконечном количестве элементов U.

U

A = µ₁/y₁+ µ₂/y₂ +… +µ_n/y_n = ∑µ_i/y_i; (i = 1,…n)– при конечном количестве элементов U.

Пример: Пусть U – это числа U = {1,2,…,10}, а нечеткое множество А зададим понятием «несколько».

А _{<несколько>} 0,4/2 + 0,7/3 + 0,2/8 + 0,7/9 (3 ближе к понятию «несколько»).

- равенство по определению. µА(у) = [0;1].

Чем больше степень принадлежности µ(А), тем выше степень коэффициента. Выбор µ (коэффициентов) субъективен. В этом основная проблема нечетких множеств.

В _<много> 0,1/2 + 0,3/3 + 0,5/4 + 0,7/8 + 1/10.

Пример:

U = {пинчер, гончая, овчарка, бульдог}.

A _<злой> 0,9/пинчер + 0,2/гончая + 0,5/овчарка + 0,6/бульдог;

A _{<добрый>} 0,1/пинчер + 0,8/гончая + 0,5/овчарка + 0,4/бульдог;

7.1.2. Операции над нечёткими множествами.

Над нечеткими множествами выполняются те же операции, что и над обычными множествами.

Пусть:

U=(u ₁, u ₂, u ₃, u ₄, u ₅, u ₆, u ₇)

А = {(0,6/u₁); (0,4/u₂); (0,3/u₃); (0,8/u₄); (0,5/u₅); (1/u₆); (0,6/u₇)}

Рис.57. Функция принадлежности нечёткого множества А к элементам множества U

B = {(0,9/u₁); (0,2/u₂); (1/u₃);(0,5/u₅); (0,8/u₆); (1/u₇)}

Рис.58. Функция принадлежности нечёткого множества В к элементам множества U

Операции:

1.. Объединение: (А 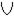В) òµ_А(у) µ_В(у)/у, где max из двух µ; µ_А(у) 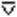µ_В(у) = max

U

(µ_А(у), µ_В(у)), тогда А 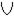В = {(0,9/u₁); (0,4/u₂); (1/u₃); (0,8/u₄); (0,5/u₅); (1/u₆); (1/u₇) }

2. Пересечение: А ∩В ò µ_А(у) µ_В(у)/у, где µ_А(у) µ_В(у) = min (µ_А(у), µ_В(у)).

U

А ∩В = {(0,6/u₁); (0,2/u₂); (0,3/u₃); (0,5/u₅); (0,8/u₆); (0,6/u₇)}.

3. Дополнение (отрицание): 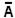ò (1 - µ_А(у))/у; 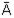={(0,4/u₁); (0,6/u₂); (0,7/u₃); (0,2/u₄); (0,5/u₅); (0,4/u₇)}; U

4. Сумма: А + В (А 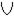В) – (А ∩В); А + В = {(0,3/u₁); (0,2/u₂); (0,7/u₃); (0,8/u₄); (0,2/u₆); (0,4/u₇)}

5. Разность: А – В А ∩ 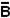; А – В = {(0,1/u₁); (0,4/u₂); (0,5/u₅); (0,2/u₆)}

6. Произведение: А*В òµ_А(у)*µ_В(у)/у; А*В = {(0,54/u₁); (0,8/u₂); (0,3/u₃); (0,25/u₅); (0,8/u₆); (0,6/u₇)} U

7. Возведение в степень: A^α òµ^α_А(у)/у, α > 0.

U

8.Концентрирование: CON(A) A² Уменьшает степень принадлежности элемента нечеткого множества.

9. Растяжение: DIL (A) A ^0,5 Увеличивает степень принадлежности элемента нечеткого множества.

Пример:

Введем множество U = {1, 2, 3, 4, 5}

«Слабый студент» 1/1 + 0,8/2 + 0,6/3 + 0,3/4 + 0,2/5;

«Хороший студент» 0/1 + 0,4/2 + 0,6/3 + 1/4 + 0,8/5;

«Отличный студент» 0/1 + 0/2 + 0,4/3 + 0,5/4 + 1/5;

С помощью операций над нечёткими множествами можно создать новые нечёкие множества.

«Очень слабый студент» 1/1 + 0,64/2 + 0,36/3 + 0,09/4 + 0,04/5; (применяется операция концентрирования).

«Не слабый студент» 0,2/2 + 0,4/3 + 0,7/4 + 0,8/5;

«Очень не слабый студент» 0,04/2 + 0,16/3 + 0,49/4 + 0,64/5;

«Не очень слабый студент» 0,36/2 + 0,64/3 + 0,91/4 + 0,96/5;

Достоинства:

· Можно оперировать с нечеткими множествами;

· Можно определить количество нечеткости.

Недостатки:

· Субъективность коэффициентов µ.

Дата добавления: 2015-06-27