Расчет быстро вращающихся дисков

Давление при запрессовке круглых деталей

Пусть есть две трубы: первая с внутренним радиусом а и внешним

с + , вторая с внутренним радиусом с и внешним b. Поле запрессовки первой трубы во вторую возникает контактное давление .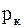

Определим величину этого давления.

Внутренняя труба сжата давлением 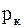. При этом ее наружный радиус уменьшается (u₁ < 0):

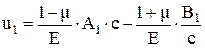
где

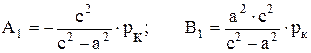
Внешняя труба растягивается давлением Р_к. Ее внутренний радиус увеличивается на величину

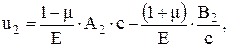
где

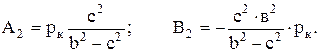
Поскольку

u₂ - u₁ = ,

после подстановки выражений для u₁ и u₂

.

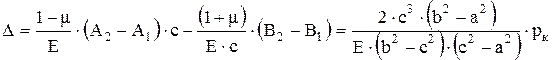Откуда

.

После определения контактного давления расчет напряжений в сопрягаемых деталях не представляет сложности.

Найдем частное решение 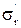системы (1…5). Повторив преобразования, аналогичного проведенные для однородной системы, приходим к уравнению

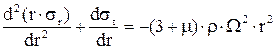. (15)

Частное решение ищем в виде правой части: . Подставляя в (15) после элементарных преобразований находим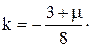

Сумма общего решения однородного уравнения и частного решения уравнения с правой частью дает

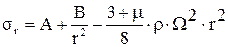. (16)

Подставив в (1) находим

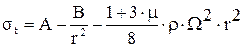. (17)

Для диска, выполненного за одно с валом, имеем граничные условия:

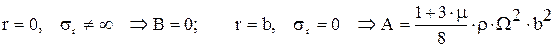
Следовательно

, .

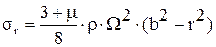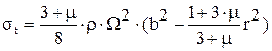Для диска, свободно посаженного на вал, имеем граничные условия:

.

После решения соответствующей системы алгебраических уравнений относительно А и В и подстановки в (16), (17), получаем

, .

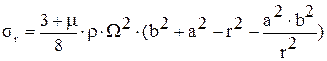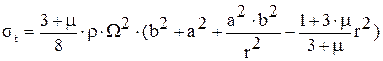Характер распределения напряжений в диске представлен на рисунке. Наиболее нагружен материал в центре диска. Поэтому в реальных конструкциях делают толщину диска t переменной и уменьшающейся к его периферии.

Задачи решены для дисков постоянной толщины. При система решается численно. Подробности - в учебниках и специальных курсах.

Дата добавления: 2015-06-27