Ряд, образованный геометрической прогрессией

Рассмотрим ряд, составленный из членов геометрической прогрессии. Напомним, что геометрической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число, не равное нулю и называемое знаменателем этой прогрессии. Геометрическая прогрессия имеет вид:

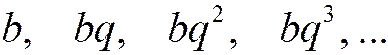
а ряд, составленный из ее членов:

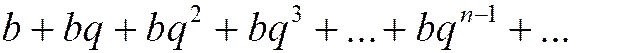
Такой ряд называется геометрическим рядом, но иногда для краткости его называют просто геометрической прогрессией. Название «геометрическая» прогрессия получила потому, что каждый ее член, начиная со второго, равен среднему геометрическому соседних с ним членов:

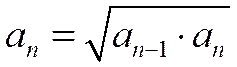, или .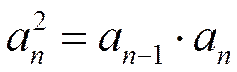

Теорема. Ряд, составленный из членов геометрической прогрессии

(1.13)

расходится при 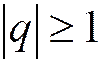и сходится при 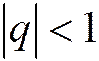, причём при 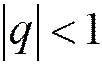сумма ряда

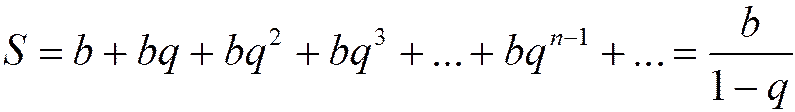(1.14)

Доказательство. Общий член ряда, как и общий член геометрической прогрессии, имеет вид: .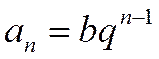

1) Если 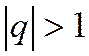, то 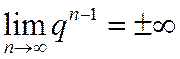, т.к. в этом случае 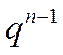– бесконечно большая величина.

2) При 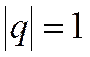ряд ведёт себя по-разному, т.к. приобретает различные виды.

При ;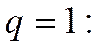

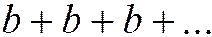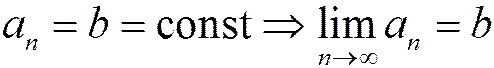, т.к. предел константы равен самой константе. Т.к. по условию теоремы 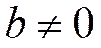, общий член ряда не стремится к нулю.

При 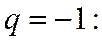; предела не существует.

Таким образом, при 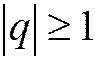не выполняется необходимое условие сходимости ряда:

.

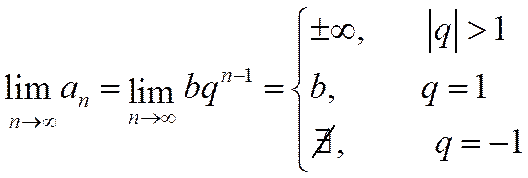Следовательно, ряд (1.13) расходится.

3) Если 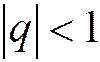, то прогрессия называется бесконечно убывающей. Из школьного курса известно, что n -ю частичную сумму ряда (1.13) можно представить в виде:

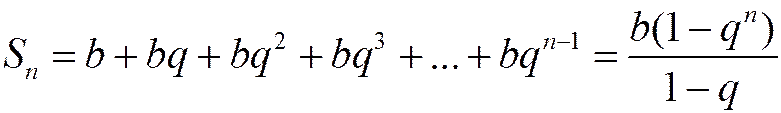. (1.15)

Найдём сумму ряда. Так как при 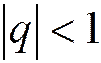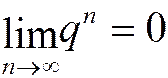(бесконечно малая величина), то

.

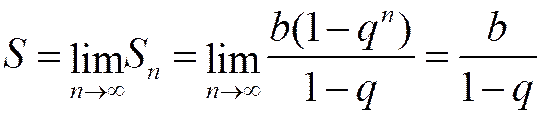Таким образом, при 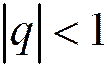ряд (1.13) сходится и имеет сумму, равную

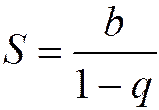. (1.16)

Это и есть сумма бесконечно убывающей геометрической прогрессии.

Пример 1º.

Рис.1.4.1

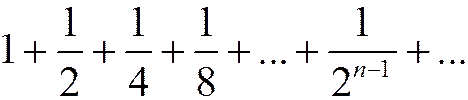=2.

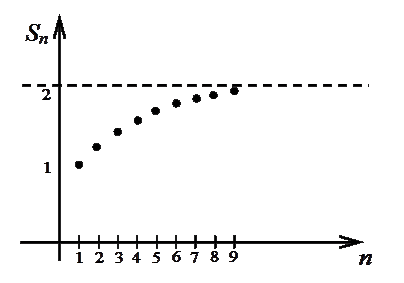
Оценим его сумму, т.е. попробуем определить, к чему стремится последовательность его частичных сумм.

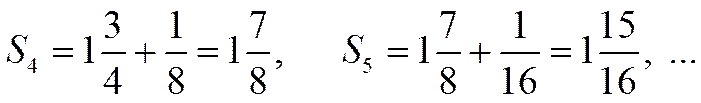
Видно, что последовательность частичных сумм стремится к числу 2 (рис.1.4.1).

А теперь докажем это. Воспользуемся тем, что данный ряд - это ряд, составленный из членов геометрической прогрессии, где 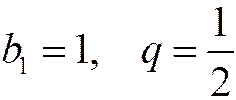. Сумма бесконечно убывающей геометрической прогрессии

.

Пример 2 º.

.

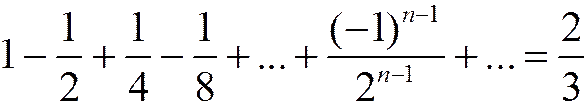Вычисляется аналогично. Поскольку многие из членов ряда в отличие от предыдущего примера имеют знак минус, то сумма оказалась меньше.

Пример 3 º.

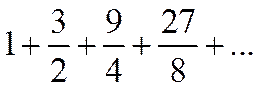
Это геометрический ряд, где 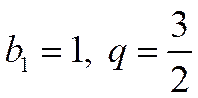>1. Такой ряд расходится.

Дата добавления: 2015-06-27