Теоретическая часть. Метод градиентного спуска

Метод градиентного спуска

Метод градиентного спуска – это классический метод поиска минимума дифференцируемой функции с аргументами, принимающими вещественные значения. Данный метод, как правило, применяется для многомерных функций, поскольку в одномерном случае существуют более эффективные методы поиска.

Как известно, градиент некоторый функции 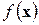в некоторой точке показывает направление локального наискорейшего увеличения функции. Этот факт используется в методах градиентного спуска (подъема).

Эти методы описываются следующей последовательностью действий:

1. Выбрать начальную точку 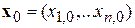. Установить номер итерации: i= 0.

2. Для текущей точки определить значение градиента:

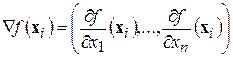. (1)

В случае если градиент не может быть вычислен аналитически, его компоненты могут быть оценены:

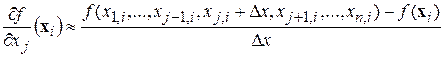. (2)

3. Определить положение следующей точки:

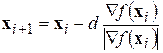, (3)

где d – параметр, определяющий скорость спуска, и положить i = i +1.

4. Перейти к шагу 2, если не выполнен критерий останова.

Существует несколько способов ввода критерия останова. Самый простой – это наложить ограничение на количество итераций. Другие способы связаны с проверкой того, что текущая точка или значение функции f меняются мало. При фиксированном шаге d изменение положения текущей точки происходит всегда на одну и ту же величину. Однако в этом случае можно проверять изменение за несколько итераций и сравнивать с d: .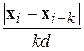

Существует также возможность адаптивного выбора шага d. Для этого на каждой итерации осуществляется выбор такого значения из 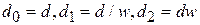(где w – некоторый параметр, как правило 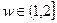), что значение функции в точке 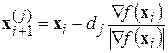минимально. Таким образом, если при большом d метод градиентного спуска «проскакивает» минимум, то d будет уменьшаться. Уменьшение d ниже заданного порога также служит критерием остановка. Напротив, на пологих участках значение d будет увеличиваться.

При условии существования глобального минимума функции f метод градиентного спуска обычно сходится (за исключением случаев, когда вдоль некоторого направления функция, монотонно убывая, стремится к некоторому конечному пределу при 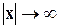). Сходимость метода обеспечивается тем, что на каждой итерации выбирается такая точка 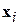, что 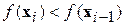. Метод, однако, не гарантирует нахождения глобального минимума, поскольку при достижении любого локального минимума метод не в состоянии определить направление на более глубокий минимум (и вообще обнаружить его существование) и останавливается в соответствии с выбранным критерием останова.

В связи с этим, выбор начальной точки может существенным образом сказываться на получаемом результате.

Метод моделирования отжига

Метод моделирования отжига предназначен для поиска глобального минимума некоторой функции 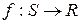, где S – некоторое пространство (необязательно непрерывное), элементы которого интерпретируются как состояния некоторой воображаемой физической системы, а значения самой функции – как энергия этой системы E = f (x) в состоянии .

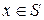В методе моделирования отжига система в каждый момент времени находится в некотором состоянии x_i, а также обладает некоторой температурой T, которая является управляемым параметром.

На каждой итерации система случайным образом переходит в новое состояние 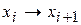. Механизм выбора нового состояния состоит из двух частей:

1. Сначала выбирается 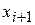в соответствии с некоторой функцией распределения 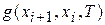. Как правило, эта функция зависит только от расстояния 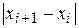, причем с увеличением этого расстояния вероятность перехода понижается.

2. После случайного выбора 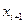проверяется вероятность перехода в это новое состояние, исходя из разности энергий и текущей температуры: 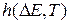, 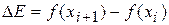. Здесь 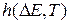показывает вероятность перехода в состояние с другой энергией. Проверка производится следующим образом: выбрасывается случайное число из диапазона [0, 1]. Если это число оказывается меньше, чем значение вероятности 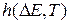, то новое состояние 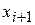принимается, в противном случае шаг 1 повторяется. Функция 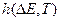, как правило, стремится к 1 при 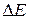, стремящемся в минус бесконечность, и стремится к 0 при 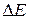, стремящемся в плюс бесконечность (то есть предпочтение в среднем отдается состояниям с меньшей энергией).

Поскольку метод моделирования отжига базируется на физических принципах, то и функции распределения вероятносте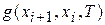й и 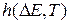также часто заимствуются из физики. В частности, достаточно популярен больцмановский отжиг, в котором:

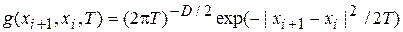, (4)

где D – размерность пространства S;

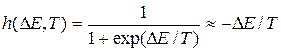. (5)

Таким образом, температура T определяет, насколько в среднем может меняться текущее состояние 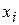, а также то, насколько в среднем может меняться энергия системы при переходе в новое состояние.

Поскольку переход в состояния с меньшей энергией более вероятен, чем переход в состояния с более высокой энергией, то система будет больше времени проводит именно в низкоэнергетических состояниях.

Чтобы обеспечить сходимость системы к некоторому состоянию с наименьшей энергией, температуру системы понижают с переходом к следующей итерации. В больцмановском отжиге применяется следующий закон понижения температуры:

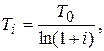(6)

где номер итерации 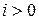. Такой закон может, однако, потребовать большое число итераций, особенно при больших значениях начальной температуры T ₀, в связи с чем используется более быстрое понижение температуры:

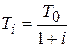. (7)

Начальная температура неявно задает область, в которой будет осуществляться поиск глобального минимума, а также определяет необходимое для сходимости число итераций.

Дата добавления: 2015-06-27