Экспериментальная часть. В данной работе проводят сравнительный анализ методов градиентного спуска и моделирования отжига

В данной работе проводят сравнительный анализ методов градиентного спуска и моделирования отжига. Суть сравнительного анализа в данном случае заключается в построении графиков зависимости точности находимого решения от числа итераций для обоих методов и сопоставлении этих графиков для функций различных типов. Для этого необходимо последовательно выполнить следующие действия.

1. Реализовать методы градиентного спуска и моделирования отжига и описать детали выбранной реализации.

2. Для нескольких вогнутых (обладающих единственным минимумом) функций построить графики зависимости 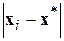(где 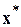- истинное положение глобального минимума) от номера итерации i для обоих методов. Выбранные для исследования функции должны различаться средним значением модуля градиента (крутизной). Следует обратить внимание на выбор начальной точки , которая должна отличаться от искомого минимума 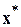. В методе моделирования отжига следует также обратить внимание на задание начальной температуры T ₀ и ее влиянии на скорость сходимости.

3. Для нескольких функций с многими локальными минимумами определить условия сходимости обоих методов к глобальному минимуму. Для градиентного спуска определить, с какой вероятностью метод сходится к глобальному минимуму при случайном выборе (из некоторого фиксированного диапазона) начальной точки. Для метода моделирования отжига определить, какая начальная температура обеспечивает сходимость к глобальному минимуму. Для исследования следует брать функции с разным числом минимумов.

4. Проанализировать полученные результаты. Определить предпочтительность использования каждого из методов при поиске минимума функции с одним и многими минимумами, опираясь на скорость сходимости и на легкость нахождения глобального минимума. Сделать выводы по работе.

Литература

1. Назаров, А.В. Нейросетевые алгоритмы прогнозирования и оптимизации систем / А.В. Назаров, А.И. Лоскутов. – СПб.: Наука и Техника, 2003. – С. 237-238.

Вопросы для самопроверки:

1. Какое условие сходимости метода градиентного спуска к глобальному минимуму?

2. Каков смысл параметра температуры в методе моделирования отжига?

3. На что влияет выбор начальной температуры в методе моделирования отжига?

4. Пусть в методе моделирования отжига используется закон уменьшения температуры 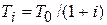и пусть 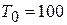. Сколько требуется итераций, чтобы обеспечить точность нахождения минимума 10^-4.

5. Какое основное отличие методов моделирования отжига и градиентного спуска?

6. Как можно было бы совместно использовать два этих метода?

Вариант 2

Задание по работе:

1. Изучить теоретическую часть работы.

2. Реализовать генетический алгоритм поиска минимума.

3. Для функций двух видов: вогнутой и с вторичными минимумами применить генетические алгоритмы и оценить скорость сходимости и возможность нахождения глобального минимума в зависимости от размера начальной популяции и скорости мутаций.

Дата добавления: 2015-06-27