Пучки труб 1 страница

Одиночная труба

Средний по окружности коэффициент теплоотдачи рассчитывают по формуле

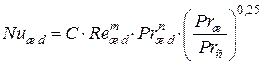. (1.12)

Физические параметры жидкости берут при температуре набегающего потока.

Эмпирические коэффициенты зависят от :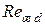

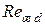
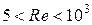
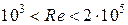
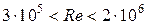
C	0,5	0,25	0,023
m	0,5	0,6	0,8
n	0,38	0,38	0,37

Расчётные формулы дают значения коэффициента теплоотдачи для третьего и последующих рядов труб.

При 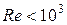для коридорных и шахматных пучков

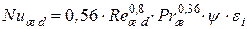. (1.13)

При 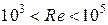используют формулу

. (1.14)

Для шахматных пучков 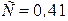; ; для коридорных ; .

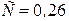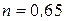Скорость жидкости берут в минимальном сечении пучка.

При обтекании пучков капельной жидкостью физические параметры жидкости выбирают при средней температуре жидкости в пучке 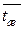, а значение 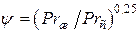. При обтекании пучков газом физические параметры для формулы (1.14) выбирают при температуре 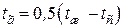, а значение .

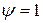Поправочный коэффициент 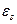учитывает влияние поперечного и продольного шагов.

Для шахматного пучка

при ,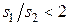

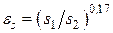при .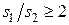

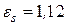Для коридорного пучка

.

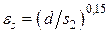Коэффициент 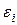учитывает более низкую теплоотдачу в первом и втором рядах труб. При невысокой или неизвестной степени турбулентности потока перед пучком значения 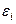находят по таблице:

Расположение труб	Номер ряда
Шахматное	0,6	0,7
Коридорное	0,6	0,9

Средний для всего пучка коэффициент теплоотдачи находят по формуле

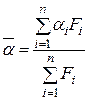. (1.15)

где i – номер ряда;

F_i – площадь поверхности теплоотдачи ряда.

Если поверхности теплоотдачи рядов одинаковы, то средний по пучку коэффициент теплоотдачи находят по формуле

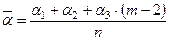, (1.16)

где n – количество рядов труб вдоль потока.

2.4. Свободная конвекция

Большая часть формул имеет вид

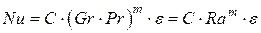. (2.1)

Определяющий линейный параметр в этой формуле выбирают в зависимости от формы и расположения поверхности теплопередачи. Физические параметры жидкости 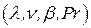берут при "граничной" температуре

.

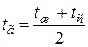Коэффициенты C и m зависят от режима движения жидкости, определяемого критерием Рэлея.

Для вертикальной поверхности теплопередачи

при , ;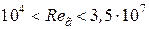

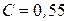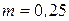при , .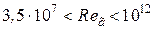

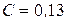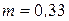Для горячей горизонтальной поверхности, обращённой вверх,

при , ;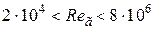

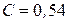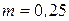при , .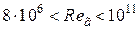

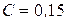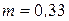Для горячей горизонтальной поверхности, обращённой вниз

при , .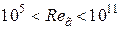

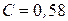Для горизонтального цилиндра

при , .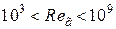

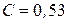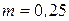Иногда в качестве определяющей удобнее брать не граничную температуру t_г, а температуру окружающей среды t_ж. В этом случае коэффициенты C и m в уравнении (2.1) такие:

для горизонтальных цилиндров

при , ;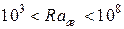

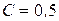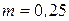для вертикальных поверхностей

при , ;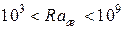

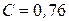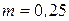при , .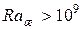

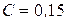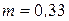Если не один из указанных выше вариантов расчёта не подходит, можно пользоваться обобщённой формулой М.А.Михеева, применимой для различных геометрических систем

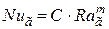, (2.2)

координаты которой выбирают из таблицы

Ra	10^-4…10^-3	10^-3…5×10^2	5×10^2…2×10^7	2×10^7…10^13
C	0,5	1,18	0,54	0,135
m		0,125	0,25	0,33

При этом коэффициент теплопередачи для горячей горизонтальной поверхности, обращённой вниз, уменьшают на 30%.

Для капельных жидкостей значения Nu по формулам (2.1) и (2.2) следует умножить на поправочный коэффициент

.

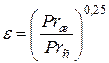3.5. Конденсация пара

При конденсации на одиночной горизонтальной трубе средний по периметру коэффициент теплоотдачи

, (3.1)

где t_н и t_с – температуры насыщения и стенки трубы соответственно.

Для пучка труб средний по пучку коэффициент теплоотдачи рассчитывают по приближённой формуле:

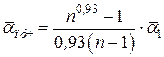, (3.2)

где n – число труб по вертикали;

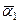– коэффициент теплоотдачи для одиночной трубы.

При конденсации пара на вертикальной стенке сначала рассчитывают критерий Григулля:

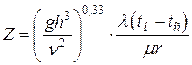, (3.3)

а затем – средний по высоте безразмерный коэффициент теплоотдачи (критерий Рейнольдса):

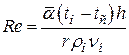, (3.4)

где h – высота стенки.

При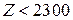

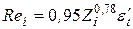, (3.5)

где ,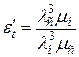

l_с и m_с – параметры конденсата при температуре стенки;

l_н и m_н – параметры конденсата при температуре насыщения.

При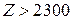

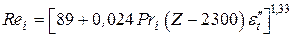, (3.6)

где .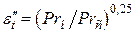

4.6. Тепловое излучение

4.6.1. Лучистый теплообмен между телами, разделёнными диатермической средой

4.6.1.1. Замкнутая система из двух серых тел

Результирующий поток для второго тела:

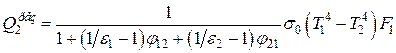. (6.1)

4.6.1.2. Замкнутая система из трёх серых тел

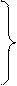Результирующие потоки для всех поверхностей находят по формулам:

(6.2)

где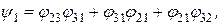

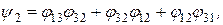
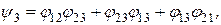
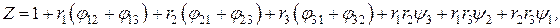
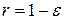– отражательная способность.

4.6.1.3. Замкнутая система трёх поверхностей, из которых 1 и 2 абсолютно чёрные, а 3 – адиабатная (рис. 6.1.)

Рис. 4.1. Система из трёх тел; а – "в собранном", б – "в разомкнутом" виде

Результирующий поток для второй поверхности находят по формуле

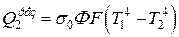, (4.3)

где 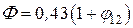– коэффициент диафрагмирования;

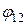– угловой коэффициент внутренней (F₁) площади поперечного сечения отверстия на наружную (F₂).

4.6.2. Теплообмен с участием излучающего газа

4.6.2.1. Эффективная длина луча

Для расчёта эффективной длины луча, необходимо при использовании графиков Хоттеля (табл.) имеются следующие формулы:

"универсальная"

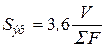, (4.4)

а для излучающего газа в пучке труб

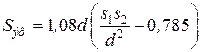, (4.5)

где V – объём газа;

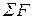– сумма поверхностей, ограничивающих газовый объём;

d – диаметр труб в пучке;

s₁ и s₂ – поперечный и продольный шаги труб.

4.6.2.2. Теплообмен газа с серой замыкающей поверхностью (оболочкой)

Результирующий поток излучения, получаемый поверхностью, рассчитывают по формуле

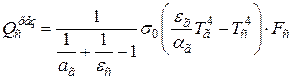, (4.6)

где 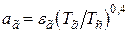– поглощательная способность газа.

Для приближённых расчётов можно считать газ серым. Тогда 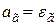, и формула (6.6) упрощается:

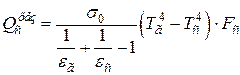. (4.7)

4.6.2.3. Теплообмен в замкнутой системе из двух поверхностей: вогнутой (2) и невогнутой (1), заполненной серым газом

Для случая, когда поверхность 2 адиабатная результирующий поток излучения на поверхность 1 рассчитывают по формуле В.Н.Тимофеева:

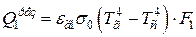, (6.8)

где 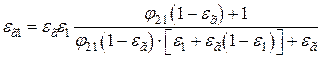– приведённая степень черноты;

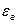– степень черноты газа;

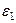– степень черноты тепловоспринимающей поверхности;

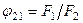– угловой коэффициент адиабатной поверхности на тепловоспринимающую.

Рис. 6.2.

Таблица 1.

Соотношение между единицами измерения МКГСС и СИ

Сила	1 кгс = 9,81 Н
Давление	1 кгс/см^2 = 0,981×10^5 Па 1 бар = 10^5 Па
Динамическая вязкость	1 кгс×с/м^2 = 0,98 Па×с
Теплопроводность	1 ккал/м×ч×^оС = 1,163 Вт/(м×К)
Коэффициент теплоотдачи	1 ккал/м^2×ч×^оС = Вт/(м^2×К)
Коэффициент излучения	1 ккал/м^2×ч×К^4 = Вт/(м^2×К^4)
Энтальпия, теплота фазового перехода	1 ккал/кгс = 4,187 кДж/кг

Таблица 2.

Физические свойства различных технических материалов

Материал	Влажность массовая W, %	Плотность r, кг/м^3	Температура t, ^оС	Коэффициент теплопроводности l, Вт/(м×^оС)	Теплоёмкость c, кДж/(кг×^оС)
Антрацит	–		–	0,328	0,947
Асфальт			0-30	0,60-0,74	1,7
Бакелитовый лак	–		–	0,29	–
Бетон с каменным щебнем				1,3	0,84
Бетон сухой				0,84	0,84
Железобетон				1,55	0,84
Шлакобетон				0,70	0,80
Бумага обыкновенная	Воздушно-сухая	–		0,14	0,5
Вата хлопчатобумажная	Воздушно-сухая			0,042	–
Гипс формованный				0,43	0,84-0,92
Глина	15-20	2000-1600		0,9-0,7	0,84
Глина огнеупорная				1,0
Гравий	Воздушно-сухой			0,36	–
Грунт подзолистый	–			0,279	0,84
Грунт суглинок	–			1,49	1,15
Замазка Менделеева	–		–	0,129	–
Дельта-древесина	Воздушно-сухая	–	35-70	0,21	–
Дерево:
дуб поперёк волокон	6-8		0-15	0,20-0,21	2,4
дуб вдоль волокон	6-8		12-50	0,35-0,43	2,4
сосна поперёк волокон			0-50	0,14-0,16	2,7
сосна вдоль волокон		–	20-25	0,35-0,41	2,7
фанера клееная				0,15	2,5
Древесный уголь кусковой	Естественная влажность			0,074	–
Картон	Воздушно-сухой	–		0,14-0,35	1,5
Кембрик лакированный	–	–		0,157	–
Кирпич:
красный машинной формовки	Воздушно-сухой			0,77	0,88
ручной	Воздушно-сухой			0,70	0,88
силикатный	Воздушно-сухой			0,81	0,84
Кладка из красного кирпича:
на холодном растворе	Воздушно-сухая			0,81	0,88
на тёплом растворе	Воздушно-сухая			0,67	0,84
Кладка из силикатного кирпича:
на холодном растворе	Воздушно-сухая			0,87	0,84
на тёплом растворе	Воздушно-сухая			0,76	0,80
Кладка бутовая из камней средней плотности	Воздушно-сухая			1,28	0,88
Карболит чёрный	Воздушно-сухой			0,138	–
Кокс порошкообразный				0,191	1,2
Котельная накипь:
богатая гипсом		2000-2700		0,7-2	–
богатая известью		1000-2500		0,15-2	–
богатая силикатами		300-1200		0,08-0,23	–
Кварц кристаллический:
поперёк оси	–	–		7,2	–
вдоль оси	–			13,6	–
Ламповая сажа	Воздушно-сухая			0,07-0,12	–
Лёд	–			2,2	2,3
Льняная ткань	Воздушно- сухая	–	–	0.088	–
Мел	Воздушно- сухой			0,93	0,88
Миканит	Воздушно- сухой	–		0,21-0,41	–
Мрамор	Воздушно- сухой			1,30-3	0,92
Органическое стекло (плексиглас)	–	–		0,184	–
Парафин	–			0,27	–
Песок речной мелкий	–			0,326	0,797
Песок речной крупный	–		–	0,512	1,02
Резина: твёрдая обыкновенная	–		0-100	0,157-0,160	1,4
мягкая	–	–		0,13-0,16	1,4
пористая	воздушно-сухая		–	0,050	–
Сера ромбическая	То же	–		0,28	0,762
Сланец	Воздушно-сухой	–		1,49	–
Слюда (поперёк слоёв)	–	2600-3200		0,47-0,58	0,88
Снег свежевыпавший	–		–	0,1
Снег уплотнённый	–		–	0,47
Стекло:
зеркальное	–		0-100	0,78-0,88	0,778
обыкновенное	–		–	0,74+0,001· t	0,67
термометрическое	–			0,97	–
пирекс	–	–		1,0	–
пирекс	–	–		1,55	–
кварцевое	–		–180	0,71	–
кварцевое	–	–	–100	1,1	–
кварцевое	–	–		1,35	–
кварцевое	–	–		1,42	–
кварцевое	–	–		1,49	–
кварцевое	–	–		1,60	–
кварцевое	–	–		1,76	–
кварцевое	–	–		2,08	–
кварцевое	–	–		2,40	–
кварцевое	–	–		2,72	–
кварцевое	–	–		3,05	–
молибденовое	–	–	–	0,81+0,001· t	–
Текстолит	–	1300-1400		0,23-0,34	1,46-1,51
Уголь каменный	–		–	0,186	1,30
Уголь бурый	–		–	0,254	1,13
Фарфор	–			1,0	1,1
Фарфор	–			1,97	1,1
Фибра красная	–		20-100	0,47-0,50	–
Фибролит		360-440		0,073-0,128	–
Целлулоид	–			0,21	–
Шелк	–		0-93	0,043-0,06	–
Шерстяная ткань			–	0,052	–
Эбонит	–			0,157-0,174	–
Штукатурка:
известковая	6-8			0,70	0,84
цементно-песчаная	5-6			1,2	0,84

Таблица 3.

Коэффициент теплопроводности теплоизоляционных материалов

Материал	Плотность, кг/м^3	Коэффициент теплопроводности в сухом состоянии в зависимости от температуры, Вт/(м×^оС)	Допустимая температура, ^оС
Альфоль	3-10	0,052+0,00014 t
Асбест		0,106+0,00019 t
	0,094+0,00019 t
	0,084+0,00016 t
	0,074+0,00016 t
	0,060+0,00016 t
Асбестовая бумага		0,177+0,00014 t
	0,157+0,00014 t
	0,134+0,00014 t
Асбоцементные плиты		0,088+0,00013 t
		0,079+0,00012 t
Асбестовый картон		0,157+0,00014 t
Асбестовый войлок		0,09+0,00019 t
	0,052+0,00016 t
Асбестовый шнур (кручёный)		0,178+0,000098 t
Асбестовый шнур		0,17 при 100^оС	450 без хлопка, 200 с добавкой хлопка
	0,15 при 100^оС
	0,10 при 100^оС
Асбест распущенный, VI сорт		0,11+0,00019 t
Асбест распущенный, III сорт		0,087+0,00024 t
Асбозурит класса А		0,15 при 100^оС
	0,13 при 100^оС
	0,09 при 100^оС
Асбозурит класса Б		0,23 при 100^оС	–
	0,21 при 100^оС	–
	0,19 при 100^оС	–
Асбозонолит	500-550	0,143+0,00019 t
Асбослюда	580-650	0,134+0,00015 t
Асботермит	550-570	0,109+0,000145 t
Войлок шерстяной		0,05+0,00020 t
Вермикулит (плиты)	350-380	0,08+0,00020 t
Вулканит (плиты)		0,078+0,0002 t
Газостекло (пеностекло)		0,107+0,00020 t
	0,087+0,00019 t
	0,073+0,00019 t
Диатомовые обоженные изделия		0,2+0,0003 t
	0,17+0,0003 t
	0,13+0,0002 t
	0,087+0,00022 t
	0,064+0,00020 t
Зола	450-800	0,1-0,17 при 50^оС
Зонолит зернистый		0,072+0,000262 t
Камышит (плиты)	260-360	0,1 при 0^оС
Минеральная вата		0,071+0,00019 t
	0,06+0,000180 t
	0,052+0,000178 t
	0,05+0,00017 t
	0,041+0,00017 t
Минераловатный войлок на битумной связке		0,064+0,000147 t
Минераловатный плиты на битумной связке		0,064+0,00015 t
Мипора	17,5	0,038 при 30^оС
Новоазбозурит	620-650	0,144+0,00014 t
Нювель	350-370	0,087+0,000064 t
Пенопласты (поропласты)		0,06 при 30^оС
	0,049 при 30^оС
	0,05 при 30^оС
	0,043 при 30^оС
Пенобетон		0,320 при 30^оС
	0,254 при 30^оС
	0,192 при 30^оС
	0,149 при 30^оС
	0,120 при 30^оС
	0,107 при 30^оС
Пробковые плиты	147-198	0,042-0,054 при 80^оС
Совелитовые плиты		0,08+0,0001 t
Доломитовые плиты	260-360	0,1 при 0^оС
Стекловолокно (маты)	120-200	0,040+0,0003 t
Торфяные плиты		0,067+0,00014 t
	0,060+0,00014 t
	0,052+0,00014 t
	0,045+0,00014 t
Торф сфагнум		0,128 при 30^оС
	0,11 при 30^оС
	0,087 при 30^оС
	0,070 при 30^оС
Феррон (с органическим наполнителем)	400-500	0,07 при 30^оС
Феррон (с наполнителем)	450-550	0,08 при 30^оС
Фибролит		0,122 при 30^оС
	0,1 при 30^оС
	0,09 при 30^оС
Шлак гранулированный		0,174 при 30^оС
	0,151 при 30^оС
	0,134 при 30^оС
Шлак топок парогенераторов		0,145 при 30^оС
	0,128 при 30^оС
	0,11 при 30^оС
	0,09 при 30^оС
Шлак топок парогенераторов		0,37 при 30^оС
	0,34 при 30^оС
	0,30 при 30^оС
	0,27 при 30^оС
	0,23 при 30^оС

Дата добавления: 2015-06-27