Расчет растягивающих усилий на участке набора зенитного угла с учетом влияния желобов

Можно считать доказанным [4], что желоба в наклонно направленной скважине образуются в результате термоциклического воздействия тела трубы при ее трении о стенки скважины, поэтому их ширина на этапе формирования желоба равна диаметру трубы [4].

Появление желоба вносит существенные отличия в силовое взаимодействие замка бурильных труб со стенкой скважины.

Предположим, что радиус кривизны скважины и длина трубы "позволяют" сформироваться желобу полного профиля acb (рис. 8.2). Тогда центр поверхности замка из положения O₂ переместится в точку O₃ (или, что то же амое, точка m перемесится в точку n). В результате замок коснется скважины в точках a и b. Сила F_пр, с которой труба прижата к стенке скважины, по правилу разложения результирующей силы разделится на две равные расклинивающие силы F_кл, величины которых зависят от угла β между направлениями сил F_пр и F_кл.

Рис. 8.2. Схема взаимодействия замка бурильной трубы
с кромками желоба

Из рис. 8.2 следует, что

β = arcsin (r/r_зм) = arcsin (d_тр /d_зм), (8.11)

где r и r_зм – соответственно радиусы трубы и замка. Тогда из араллелограммма сил следует, что

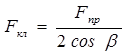. (8.12)

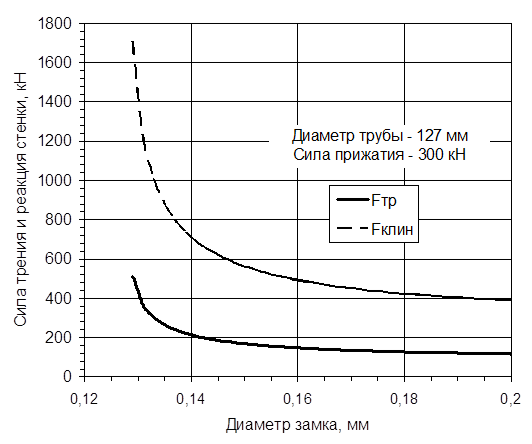
Рис. 8.3. Влияние диаметра замка на результаты силового
взаимодействия замка бурильной трубы со стенкой
скважины (коэффициент трения – 0,3).

Наличие желобов, ширина которых равна диаметру трубы, а глубина – её радиусу, создает, таким образом, "клиновой" эффект, который тем больше, чем меньше диаметр замка: с увеличением угла β увеличиваются расклинивающие силы F_кл.

Если ширина желоба h_ж больше диаметра трубы, но меньше диаметра замка, то угол β определяется по формуле:

β = arcsin (h_ж /d_зм). (8.11)^*

Видно, что с увеличением ширины желоба h_ж силы "клинового" происхождения будут возрастать.

Дополнительные силы трения, обусловленные появлением сил F_кл, составят:

. (8.13)

На рис. 8.3 приведены результаты расчета расклинивающих сил и сил трения, иллюстрирующие влияние диаметра замка при фиксированной ширине желоба.

Чтобы учесть влияние "клинового эффекта" необходимо силы трения, вызванные силами заклинивания F_кл, внести в зависимость (8.9) как дополнительные силы трения:

Q_тр.i = (1 – ψ) F_i μ + (K -1) q_т g l₀ k_a cosα_i + ψ F_i μ / cosβ, (8.14)

где ψ – доля замка в создании силы прижатия на стенку скважины со стороны трубы.

Растягивающие усилия в самом верхнем сечении участка набора зенитного угла определяются по формуле, аналогичной формуле (8.10):

.

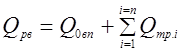Наибольшие по величине "клиновые" силы создаются при ψ = 1, когда желоб настолько глубок, что тело трубы не касается стенки скважины и вся прижимающая сила передается через замковые соединения труб.

Алгоритм расчета растягивающих сил в принципе не отличается от приведенного выше, включая организацию итерационного цикла с целью определения истинного значения растягивающей силы, за исключением того, что вместо формулы (8.9) используется формула (8.14).

На рис. 8.4 приведены результаты расчета растягивающих усилий в пределах участка набора зенитного угла. Показано также (с целью оценки величин прижимающих усилий), как по мере набора зенитного угла изменяется удельная прижимающая сила.

Рис. 8.4. Изменение удельной прижимающей (поперечной) и
растягивающей сил на участке набора зенитного угла (сверху вниз).

Условия расчета: R = 400 м; максимальный угол – 30⁰; начальное усилие в нижнем сечении участка набора – 1000 кН; коэффициент ψ = 1.

Сравниваются усилия: в покоящейся колонне; при отсутствии клинового эффекта (при отсутствии желоба); при расчёте силы с клиновым эффектом, но без уточнения в цикле; при расчете с уточнением с помощью итерационного цикла.

Точные результаты получены после трехкратного уточняющего расчета с использованием возможностей программы Excel.

Анализируя данные графика можно обнаружить, что в верхнем сечении:

- разница в усилиях между покоем и подъемом при отсутствии желоба составляет 170 кН (17 тс);

- при наличии желоба усилие при подъеме возросло на 108 кН;

- разница между приближенным и точным решением составила 35 кН (около 3%).

Такие результаты расчётов вполне согласуются с практическими данными.

При определении запасов прочности в потенциально опасных сечениях необходимо учитывать гидравлическую силу от перепада давления на долоте и забойном двигателе, если последний используется для бурения.

Контрольные вопросы:

А. Почему при наличии желобов силы трения при движении труб на участке искривления возрастают?

Б. Почему и как изменяются силы трения при изменении диаметра замка при постоянной ширине желоба?

В. Как будут изменяться силы трения при увеличения ширины желоба?

Г. При склонности пород к желобообразованию какие диаметры замков предпочтительнее?

Д. При каких условиях возможен прихват труб в желобах?

Е. Влияют ли силы растяжения на величину сил трения в желобах?

Ж. Как изменяются силы трения в желобах по мере увеличения глубины желоба?

Дата добавления: 2015-06-27