Теория объемных компрессоров 1 страница

2 ПРИНЦИП РАБОТЫ И КОНСТРУКТИВНЫЕ ЭЛЕМЕНТЫ

ПОРШНЕВЫХ КОМПРЕССОРОВ

Компрессорная установка, оборудованная поршневыми объемными машинами состоит из следующих элементов: компрессор (генератор сжатого газа), электродвигатель, вспомогательное оборудование, включающее фильтры, охладители, водо- и маслоотделители, воздухосборники, градирни, насосы. Эти элементы располагаются в компрессорной станции.

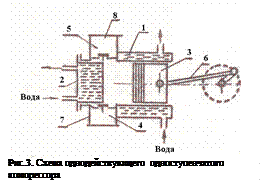При работе поршневого компрессора (рис.3) основной подвижный элемент в рабочей камере поршень 3 совершает возвратно-поступательное движение от кривошипно-шатунного механизма. При движении поршня вправо пространство между поршнем и крышкой увеличивается, давление в цилиндре уменьшается. При определенной разности давлений в цилиндре и во внешней среде открывается всасывающий клапан 4. Газ через патрубок 7 поступает в цилиндр. При обратном движении поршня давление в цилиндре повышается и всасывающий клапан закрывается. Далее газ сжимается до величины несколько большей давления в нагнетательном трубопроводе 8. После достижения разности давлений достаточной для преодоления противодавления открытию, нагнетательный клапан 5 открывается и происходит выталкивания сжатого газа при дальнейшем движении поршня до крайнего положения. Затем рабочий цикл повторяется.

Внутренние стенки рабочего цилиндра 1 компрессора и поршень смазываются во время работы компрессорным маслом, которое подается к трущимся поверхностям насосом-лубрикатором. Отверстие для подачи масла располагается близко к середине цилиндра, чтобы масло попадало в конце процесса всасывания. В настоящее время существуют бессмазочные поршневые уплотнения в компрессорах.

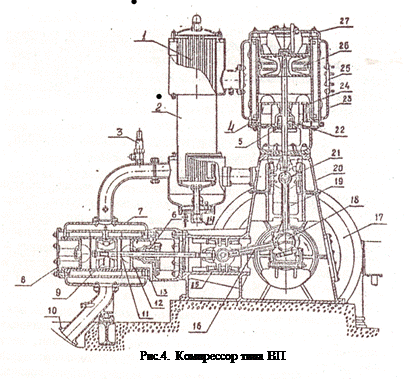
В компрессорах двухстороннего действия рабочие камеры расположены в одном цилиндре, но с разных сторон поршня. В таком компрессоре обязательна установка крейцкопфа, с которым соединяется кривошипно-шатунный механизм, а клапаны устанавливаются с двух сторон цилиндра. Для примера на рис.4 представлен разрез компрессора типа ВП.

В зависимости от характера работы и назначения все детали компрессора можно разделить на несколько групп: а) группа механизма движения - рама 20 с коренными подшипниками, коленчатый вал 18 с маховиком 17, шатуны 19 и 16, крейцкопфы 15 и 21;

б) цилиндровая группа – цилиндры 7 и 23 с крышками 8, 12, 24 и 27, сальники 6 и 22; патрубки - всасывающий 25 и нагнетательный 10; в) поршневая группа – поршни 9 и 26 с поршневыми кольцами, штоки 5 и 11; г) система охлаждения – промежуточный охладитель газа 2 с пучком труб 1, по которым циркулирует вода с подводом воды 14, охлаждающие рубашки цилиндров 4 и 13; д) группа распределения – самодействующие клапаны; е) система регулирования – предохранительный клапан 3, устройства для поднятия всасывающих клапанов, цилиндры дополнительных вредных пространств с клапанами включения; ж) система смазки – масляные насосы, масляные фильтры, маслопроводы, охладители и отстойники для масла.

3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИЧЕСКИХ

ПРОЦЕССОВ В КОМПРЕССОРАХ

Изменение состояния газа в результате подвода или отвода энергии называется термодинамическим процессом. Многие реальные газы, состояние которых достаточно далеко от сжижения, подчиняются основным законам термодинамики идеальных газов, которые принято выражать зависимостями для массы 1 кг данного газа или смеси газов. Известное уравнение Менделеева-Клайперона, связывающее основные параметры состояния, приведенное к 1 кг, имеет вид уравнения (10).

pv = RT. (10)

Отсюда можно написать уравнение состояния газа

p ₁ v ₁= RT ₁; p ₂ v ₂= RT ₂ и т.д. (11)

Закон сохранения энергии применительно к термодинамическим процессам, протекающим в полостях компрессора, выражается первым законом термодинамики.

Первый закон термодинамики представляется аналитическими выражениями для определения энергии в формах, не проявляющихся в механическом движении, а в форме приращения внутренней энергии и в форме тепла.

Математически первый закон термодинамики для бесконечно малого изменения состояния 1 кг газа имеет вид

dq = du+dl = du+ pdv; (12)

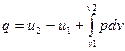, (13)

где q – количество тепла, которым 1 кг газа обменивается с окружающей средой, т.е. которое подводится или отводится от него в процессе изменения состояния, Дж/кг; u ₂ – u ₁ - изменение внутренней энергии газа, т.е. тепло, идущее на нагрев или охлаждение газа, Дж/кг; 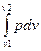- работа совершаемая над газом или производимая

1 кг газа, Дж/кг.

Уравнение (13) выражает первый закон термодинамики: количество тепла, сообщенное газу, частично идет на повышение внутренней энергии газа, а часть его может быть использована для совершения внешней механической работы расширения при переменном объеме.

В уравнении (13), исходя из условия покоящейся системы, отсутствуют составляющие внешней механической работы газа как сумма потенциальной и кинетической энергии. Потенциальная энергия положения газа на разных уровнях в компрессоре ничтожно мала, а кинетическая энергия в рабочей полости охлаждаемых компрессоров считается также малой, и учитывается только в неохлаждаемых компрессорах - центробежных и осевых.

В технике всегда стремятся к количественному выражению закономерностей в виде математических соотношений между физическими величинами. Первый закон термодинамики, как видно из уравнения (13) устанавливает количественную связь между тремя параметрами – теплом, работой и внутренней энергией.

При изучении теории компрессоров используются известные из термодинамики понятия и величины массовой удельной теплоемкости.

Удельная теплоемкость при постоянном объеме, т.е. когда подводимое к системе тепло расходуется на повышение только внутренней энергии системы dq_v =du. Отсюда изохорная теплоемкость, Дж/(кг∙град)

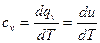. (14)

Известно, что в общем случае, работа при изменении объема и работа при изменении давления совместно выражаются, как pdv+vdp=d(pv). т.е. их сумма представляет полный дифференциал параметра состояния.

Подставив в уравнение (12) значение pdv =d(pv)-vdp, выражение первого закона термодинамики в более общем виде примет вид

dq = du+d(pv)-vdp= d(u+pv) –vdp,

или

dq =di –vdp, (15)

где i= u+pv = u +RT - энтальпия системы, Дж/(кг·град).

Таким образом, удельная энтальпия представляет собой сумму удельной внутренней энергии системы и произведения давления на удельный объем газа.

Из уравнения (15) следует, что если в системе поддерживается постоянное давление, т.е. dp = 0, то все подводимое тепло пойдет на приращение энтальпии

di=dq_p=du+pdv. (16)

Отсюда теплоемкость при постоянном давлении

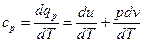. (17)

Удельные теплоемкости реальных газов c_p и c_v, как видно из выражений (14) и (17), являются функциями температуры. Однако практически в ограниченном диапазоне температур, встречающихся при работе компрессоров, эта зависимость незначительна и в обычных инженерных расчетах принимают средние значения теплоемкостей постоянными, т.е. c_p = const и c_v = const.

Заменив первый член правой части уравнения (17) через выражение

(14), а последний член выражением (10), получим другое выражение основного закона термодинамики – уравнение Майера

c_p = c_v +R. (18)

Первый закон термодинамики говорит о неуничтожимости энергии, т.е. утверждается, что происходит только преобразование энергии из одной формы в другую. Для любых энергетических преобразований всегда можно написать уравнение баланса. Однако из уравнения первого закона нельзя установить, можно ли любой вид энергии преобразовать в любой другой вид. Второй закон термодинамики, отвечая на поставленные вопросы, определяет направление протекания термодинамических процессов, накладывает определенные качественные и количественные ограничения на процессы.

Второй закон термодинамики говорит о том, что не всякая форма энергии может быть преобразована в любую другую форму энергии, а та, которая преобразуется, не вся может быть преобразована в любую другую форму энергии.

По направлению различают обратимые и необратимые процессы. Опытом установлено, что реальные процессы в природе необратимы и могут протекать самопроизвольно только в одном направлении.

Обратимый процесс рассматривается как идеализированный, предельный случай, протекающий при квазистатических изменениях состояния, для которых количество тепла и работы можно вычислить по изменению состояния системы. Обратимый процесс при возвращении системы в первоначальное состояние не вносит (или не требует) каких-либо изменений во внешней среде.

При работе компрессора неизбежны процессы теплообмена между газом, находящимся в рабочей камере, и окружающей средой, поэтому для решения инженерных задач, связанных с теплообменом, оказывается недостаточно формул, отвечающих первому закону термодинамики (для обратимых процессов). Для необратимых процессов широко используется понятие энтропии.

Энтропия, как необходимый параметр состояния системы, предложен Р. Клаузиусом в 1865 г. Энтропия является количественной формулировкой второго закона термодинамики в виде принципа необратимости.

Энтропия (от греч.) – превращение. Изменение энтропии в равновесном процессе равно отношению количества тепла dq, сообщенного системе (или отведенного от нее), к абсолютной температуре Т системы, т.е.

.

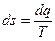Учитывая выражения (10) и (12) можно записать

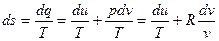. (19)

Здесь ds представляет собой полный дифференциал некоторой функции s, называемой энтропией, которая не зависит от характера процесса и определяется только начальным и конечным состоянием системы.

В теоретическом рабочем процессе компрессора имеет место два термодинамических процесса: внесение в систему механической внешней работы, затраченной на сжатие газа, и теплообмен между системой и окружающей средой. Для определения количественной оценки необратимости тепловых процессов и пользуются понятием энтропии.

Изменение энтропии пропорционально обратимо подводимому или отводимому теплу. При подводе тепла энтропия растет, а при отводе – уменьшается.

Как механическая работа изменения объема изображается площадью в координатах p-v, так и тепло можно выразить площадью в координатах T-s. Обычно в инженерных расчетах энтропию и тепло относят к массе системы, следовательно, энтропийные диаграммы строят для одного килограмма сухого газа.

На энтропийной диаграмме наносят линии состояния двух процессов (изобары и изохоры), причем площадь под этими диаграммами представляет тепло, передаваемое в процессах. Это позволяет изображать в виде площадей изменения внутренней энергии и энтальпии.

Взяв неопределенный интеграл из выражения (19), с учетом (14) можно написать

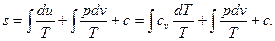(20)

Из уравнения состояния 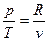получим

s = c_v ln T + R ln v + c. (21)

Постоянную интегрирования с находят из начальных условий при s = 0 для произвольно выбранных значений Т ₀ > 0 и v = v ₀

c_v ln T ₀ + R ln v ₀ + c =0 (22)

откуда c =- c_v ln T ₀ - R ln v ₀. (23)

Подставив (23) в (21) получим

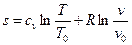. (24)

Далее для тех же начальных и конечных условий из уравнения состояния (11) можно записать p ₀ v ₀ =RT ₀ и pv =RT, тогда второй член уравнения (24) превратится в двучлен из условия, что логарифм произведения равен сумме логарифмов, так как

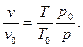(25)

Тогда

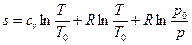(26)

или .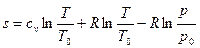

Из уравнения (18) c_p = c_v +R получим

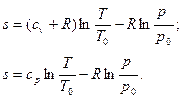(27)

Для наглядного представления энтропийной диаграммы запишем уравнение (15) в следующем виде

dq = Tds =di – vdp = c_pdT – vdp. (28)

Интегрируем последнее выражение при постоянном давлении dp= 0. Тогда приращение тепла для двух состояний системы в точках 1 и 2 составит

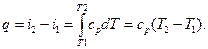(29)

Полученная разность энтальпий представляется на диаграмме в координатах Т-s в виде площади под кривой изобары, представленной на рис.5.

Таким же образом из уравнения (13)

dq = Tds = du + pdv = c_vdT + pdv (30)

после интегрирования при dv= 0 получаем

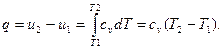(31)

т.е. на энтропийной диаграмме (рис.5) конечное приращение внутренней энергии системы также представляется площадью, но под линией постоянного объема. Как видно из уравнений (24) и (27) линии изобар и изохор в координатах Т-s представлены экспоненциальными кривыми.

Рассмотрим представленную на рис.6 систему в двух точках при разных давлениях р ₁ и р ₂ с любой, но одинаковой температурой, например Т _а = Т ₁ = Т ₂ или Т _б = Т ₁ = Т ₂ и выделим расстояние расстояния между кривыми постоянного давления р ₁ = const и р ₂ = const. Тогда, независимо от температуры из выражения (27) получим

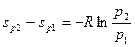. (32)

Отсюда видно, что кривые изобар располагаются на диаграмме эквидистантно. То же самое получено и для кривых изохор.

Также из выражения (27) видно, что с увеличением давления энтропия уменьшается, поэтому линии изобар более высоких давлений располагаются левее изобар с низким давлением, а из уравнения (26) видно, что изохоры с увеличением удельного объема располагаются правее малых объемов, поскольку с увеличением объема энтропия возрастает.

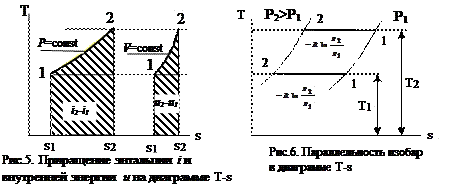
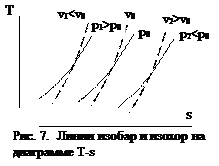
Из выражения (18) имеем c_p - c_v =R, поэтому очевидно, что c_p>c_v и изохоры (см. уравнение (26)) располагаются всегда круче, чем изобары (см. уравнение (27)). На энтропийной диаграмме (рис.7) изобары показаны сплошными линиями, а изохоры пунктирными.

Энтропийная диаграмма представляет собой масштабную сетку в координатах Т и s, причем начало координат может быть взято произвольно в пределах давлений и температур, которые характеризуют рассматриваемый процесс, например, для анализа работы воздушного компрессора при Т ₀ =273⁰К, р ₀ =10⁵ Па, v ₀ =0,8 м³/кг можно построить диаграмму в пределах изменений температуры от 248 (-25⁰С) до 573⁰К (+200⁰К), а давлений от 0,1 до 0,7 МПа.

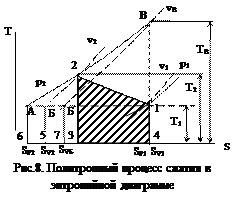
Для построения диаграмм важен выбор масштабов, чем крупнее масштаб, тем точнее расчеты (рис. 8).

Если в энтропийной диаграмме задан какой-либо теоретический процесс (показан прямой линией 1-2), что характеризуется постоянством показателя политропного процесса (п =const), то количество подведенного тепла извне и отводимого тепла от системы представляется площадкой 1-2-3-4-1 с соответствующим направлению процесса знаком, вправо, т.е. от точки 2 к точке 1 – подвод тепла с увеличением энтропии, влево, от точки 1 к точке 2 – отвод тепла и уменьшение энтропии. При расчетах по энтропийной диаграмме используются значения абсолютных температур, поэтому начало оси ординат отвечает значению Т = 0. По оси абсцисс отсчитывается разность между начальным и конечным значением энтропии, отложенной в масштабе а, поэтому начало отсчета энтропии не имеет значения. Важны только разность и масштаб энтропии, который указывается на диаграмме (1 мм = а Дж/(кг∙град∙мм). Следовательно, по энтропийной диаграмме можно определять количество отводимого тепла умножением измеренной разности энтропий s₄ –s₃ на среднюю абсолютную температуру 0,5(Т ₂ + Т ₁).

Политропный процесс описывается уравнением

сdT =dq, (33)

т.е. количество тепла, подводимого или отводимого к одному килограмму газа (при постоянном значении удельной теплоемкости политропного процесса с = const), пропорционально приращению температуры. Теплоемкость с может иметь разные значения и каждое из них соответствует определенному значению показателя политропы n, связанному с давлением и объемом газа известным уравнением

pvⁿ = const, (34)

где .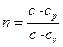

Если, как показано на рис.8, являются известными значения p ₁, v ₁, p ₂ и v ₂, то логарифмируя уравнение (34), получим

п ln v ₁ +ln p ₁ = п ln v ₂ +ln p ₂

откуда

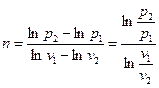. (35)

Можно показать, что из рассмотрения уравнения (32), написанного для двух изобар, и аналогичного ему для двух изохор можно уравнение (34) написать в другом виде и получить следующее отношение, представленное на энтропийной диаграмме (рис. 8)

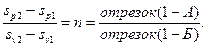(36)

Таким образом, зная начальные и конечные параметры состояния p ₁, v ₁, p ₂ и v ₂, с помощью энтропийной диаграммы можно определять показатель политропы процессов.

Далее рассмотрим широко встречающиеся в теории компрессоров термодинамические процессы, отвечающие частным значениям показателя политропы.

Адиабатный (изоэнтропный) процесс, при котором отсутствует теплообмен между газом и внешней средой, т.е. dq = 0. При этом энтропия системы не изменяется. На энтропийной диаграмме изоэнтропный процесс изменения параметров газа при сжатии пойдет по линии 1-В.

Из уравнений (28) и (30) при dq =0 можно написать с_p dT = vdp и c_vdT = - pdv. Разделив почленно и зная, что показатель адиабаты c_p/c_v = К, получим

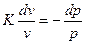. (37)

Решение данного уравнения К ln v = - ln p +ln c или

pv^K = const. (38)

Таким образом, получено основное уравнение адиабаты. Из него с помощью выражения (11) можно получить аналитическое выражение температуры в конце процесса (в точке В)

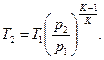(39)

Как известно, при адиабатическом процессе отсутствует теплообмен между газом и окружающей средой, поэтому все выделенное тепло при сжатии идет на приращение внутренней энергии газа и, согласно выражению (31) количество тепла в энтропийной диаграмме (рис.8) будет определяться площадью под линией постоянного объема, т.е. 4-В-Б^'-7-4, или принимая участок изохоры В- Б^' из-за малой кривизны за прямую линию, получим

,

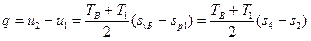где q – количество тепла, эквивалентное механической работе в компрессоре, затраченной только на процесс сжатия газа.

Изотермический процесс изменения состояния газа протекает при постоянной температуре T =const и описывается выражением

p₁v₁ = p₂v₂ =const (40)

Для поддержания постоянства температуры в процессе изменения параметров данной системы при сжатии, когда работа совершается над газом, необходимо образовавшееся тепло полностью отводить, а при расширении, когда газ производит работу, тепло необходимо подводить извне.

Количество тепла (подводимого или отводимого) при изотермическом процессе изменения состояния газа, т.е. когда du =0 и Т ₁ = Т ₂ = const, определяется из уравнения (13)

dq = dl =pdv (41)

В энтропийной диаграмме на рис.8 изотермический процесс представляется прямой 1-А и количество тепла, эквивалентное затраченной или полученной механической работе, определяется площадью 1-А-6-4-1; численно работа будет равна

q= T ₁(s_p1 – s_p2) = T ₁(s₄ – s₆). (42)

Политропный процесс сжатия применительно к теории поршневых компрессоров рассматривается как промежуточный между адиабатным и изотермическим процессами, т.е. с частичным отводом тепла от сжимаемого газа в окружающую среду. Количество тепла, которым газ обменивается с окружающей средой, определяется, как

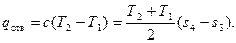(43)

Поскольку формулы (34) и (38), выражающие зависимость между параметрами газа при адиабатическом и политропном процессах, по форме написания совпадает, все другие формулы для политропы совпадают с формулами для адиабаты. Так, в формуле (39) температура при политропном процессе сжатия определяется при замене показателя k на показатель п.

4. ТЕОРЕТИЧЕСКИЕ ЦИКЛЫ В ПОРШНЕВОМ

КОМПРЕССОРЕ ОДНОСТУПЕНЧАТОГО СЖАТИЯ

Двухступенчатый поршневой компрессор соединяет в одном агрегате два последовательно соединенных одноступенчатых компрессора с промежуточным охлаждением газа между ступенями. Процессы в каждой ступени те же, что и в компрессоре одноступенчатого сжатия, поэтому сжатие газа в отдельных ступенях можно рассматривать изолированно.

Работу теоретического цикла можно вычислить на основе законов термодинамики газа, с помощью которых определяется работа, совершаемая только над газом, т.е. полезную работу компрессора. Теоретический цикл поршневого компрессора рассматривается при следующих условиях:

- основные параметры газа, поступающего в цилиндр, не изменяется в течение всего процесса всасывания и принимаются по состоянию в конце всасывания, т.е. р ₁ = const и Т ₁ = const;

- сжатие происходит по одному из теоретических процессов, т.е. при п = const;

- основные параметры сжатого газа не изменяются в течение всего процесса выталкивания его в канал нагнетания и принимаются по состоянию в конце сжатия, т.е. р ₂ = const и Т ₂ = const;

- весь газ из цилиндра выталкивается после сжатия во внешнюю сеть без остатка, т.е. вредное пространство отсутствует;

- отсутствуют аэродинамические и механические потери в компрессоре, т.е. потери в фильтре, во всасывающих и нагнетательных клапанах и трубопроводах, на трение поршня о стенки цилиндра и трение в подшипниках;

- отсутствуют утечки газа через неплотности и переход его из одной полости в другую.

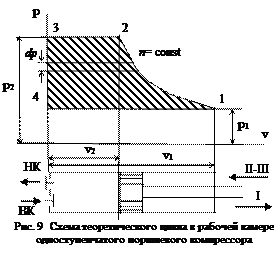
При выполнении этих условий теоретический цикл в поршневом компрессоре может быть изображен графически в координатах p-v (рис. 9). Площадь этой диаграммы выражает только затраченную работу за один теоретический цикл.

Теоретический цикл в поршневом компрессоре можно разделить на несколько фаз. При перемещении поршня вправо через открытый всасывающий клапан рабочая полость цилиндра наполняется газом, т.е. происходит процесс всасывания при p ₁ =const и Т ₁=const, который на диаграмме изображен линией 4-1. В крайнем правом положении поршень останавливается и всасывающий клапан ВК закрывается.

При обратном движении поршня газ при п = const сжимается до величины противодавления в нагнетательном трубопроводе. На диаграмме этот процесс изображен линией 1-2. В положении поршня, соответствующем точке 2, открывается нагнетательный клапан НК и при дальнейшем движении поршня сжатый газ выталкивается (нагнетается) в трубопровод. Этот процесс при p ₂ =const и Т ₂=const представлен линией 2-3.

Таким образом, теоретический цикл поршневого компрессора состоит из трех процессов: всасывания, сжатия и нагнетания. Полезная работа в компрессоре состоит из трех частей: абсолютной работы всасывания L _вс, абсолютной работы сжатия L _сж и абсолютной работы нагнетания L _нагн.

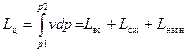. (44)

В рабочей камере поршневого компрессора эта работа совершается за два хода поршня или за один оборот кривошипа.

Для упрощения аналитических выражений, не нарушая физической картины, будем использовать всюду только абсолютные давления (а не разности давлений) и примем условно давление справа равным нулю, тогда слева будем определять так называемую абсолютную работу (с отсчетом давления от нуля). При этом работа всасывания противоположна по знаку работе сжатия и нагнетания.

Работа, совершаемая поршнем при сжатии и выталкивании, должна считаться положительной, а работа, полученная от давления источника газа при всасывании, будет отрицательной. Тогда абсолютная работа при всасывании

L _вс = - p ₁ FS ₁ = - p ₁V₁, (45)

где F – площадь поршня, S – ход поршня.

Работа, совершаемая поршнем при сжатии с изменением объема газа от V ₁ до V ₂< V ₁, т.е. с отрицательным приращением объема выразится, как

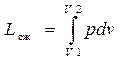. (46)

Работа, совершаемая при выталкивании

L _нагн = p ₂V₂. (47)

Согласно уравнению (44) работа в камере компрессора за один цикл (два хода поршня)

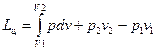. (48)

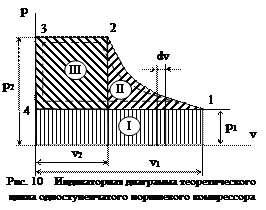
Эту работу можно представить графически в координатах p –v на рис.10, откуда видно, что алгебраическая сумма составляющих уравнения (48), т.е. I – работа всасывания, II – работа сжатия, III – работа выталкивания, представляют собой площадь 1-2-3-4-1, выражающую полезную работу за один цикл поршневого компрессора.

Для конкретного определения величины работы нужно знать закон протекания процесса сжатия, который в зависимости от условий теплообмена, может протекать при различных постоянных значениях показателя политропы п. Рассмотрим работу компрессора при известных из термодинамики теоретических процессах изотермического, адиабатического и политропного сжатия газа.

4.1 Теоретический рабочий цикл компрессора

при изотермическом сжатии

Изотермический процесс изменения состояния газа происходит при Т =const. Применительно к компрессору все тепло, образовавшееся при сжатии, должно быть отведено. Такой процесс подчиняется закону Бойля-Мариотта, т.е.

p₁v₁ = p₂v₂ = pv = const.

Тогда, работа, затраченная на изотермическое сжатие

.

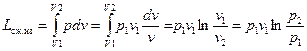Подставив это выражение в уравнение (48), получим полезную работу за цикл

,

где первый и последний члены взаимно уничтожаются, так как по условию изотермы они равны и противоположны по знаку. Тогда полезно затраченная работа в одном цикле компрессора при изотермическом сжатии равно только работе сжатия

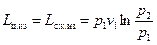(49)

Дата добавления: 2015-06-27