Компрессоры 1 страница

ЦЕНТРОБЕЖНЫЕ И ОСЕВЫЕ

11. ЛОПАСТНЫЕ КОМПРЕССОРЫ

Лопастные компрессоры выпускаются промышленностью в двух вариантах: центробежные и осевые, схемы движения газа в которых различны. Поэтому рассмотрение работы каждой машины произведено отдельно.

Принцип работы лопастных машин состоит в том, что поток газа разгоняется в рабочем колесе до высокой скорости, а, затем, в диффузоре скорость потока уменьшается и часть скоростной составляющей полной удельной работы преобразуется в статическое давление.

Преимуществом таких компрессоров перед поршневыми: в них отсутствует поступательное движение рабочего органа, а, значит, нет инерционных усилий и вибрации, которые передаются фундаменту, уменьшаются массо-габаритные показатели установки, нет загрязнения сжатого газа продуктами смазки и т.д.

11.1. Схема движения потока в рабочем колесе центробежной машины

При вращательном движении рабочего колеса поток газа в межлопаточном канале по отношению к неподвижному наблюдателю является абсолютным, а по отношению к лопатке колеса – относительным.

Струйная теория идеального колеса рассматривает движение потока через колесо, имеющего бесконечное число бесконечно тонких лопаток. В этом случае, при пренебрежении изменением потенциальной энергии, уравнение Бернулли можно представить в виде

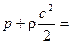const, (111)

где р – давление, Па; с – скорость движения потока, м/с; ρ – плотность среды, кг/м³.

При струйном движении план скоростей в центробежном колесе приведен на рис.33.

Примем обозначения:

u₁, u₂, - векторы окружных скоростей частиц потока соответственно на входе и выходе рабочего колеса, м/с;

w₁, w₂ – векторы относительных скоростей при входе и выходе колеса, м/с;

с₁, с₂ – векторы абсолютных скоростей при входе и выходе колеса, м/с;

α₁, α₂ – углы между направлениями векторов с и u;

β₁, β₂ – углы между направлениями векторов w и продолжением векторов u.

R ₁, R ₂ – плечо векторов с₁, с₂ относительно центра вращения;

r ₁, r ₂ – геометрические радиусы начала и конца лопатки рабочего колеса.

Следует отметить, что при расчетах часто пользуются не значениями абсолютных скоростей, а их проекциями на направление окружных скоростей и на радиальное направление, так c_{u 1} и c_{u 2} проекции векторов абсолютных скоростей на направления окружных скоростей и c_{r 1} и c_{к 2} проекции векторов абсолютных скоростей на радиальное (меридиональное) направление.

11.2. Уравнение теоретического давления

центробежного колеса компрессора

При рассмотрении теоретического процесса принимается, что передача мощности от вала колеса потоку газа происходит без потерь. В этом случае разность моментов количества движения представляет собой момент внешних сил, приложенных к потоку на участке межлопаточного канала на всем его протяжении от входа до выхода.

Момент количества движения представляет собой произведение транспортируемой массы текучего на скорость и на плечо, в данном случае М = ρ QcR.

Теоретический момент внешних сил, приложенных к потоку на участке от входной кромки до выходной, составит

М _т =ρ Q _т(c₂R₂-c₁R₁). (112)

Плечи R через геометрические радиусы колеса соответственно определяются, как R = r ·cos α. Тогда выражение (2) представится

М _т =ρ Q _т(c₂ r₂ ·cos α ₂-c₁ r₁ ·cos α ₁). (113)

Но c ₂ ·cos α ₂ = с_u2 и c ₁ ·cos α ₁ = с_u1, тогда

М _т =ρ Q _т(c_u2 r ₂-c_u1 r₁). (114)

Подведенная к валу рабочего колеса мощность без потерь преобразуется в гидравлическую мощность потока

N _т = М _т·ω = ρ Q _т(c_u2 r ₂-c_u1 r₁)·ω. (115)

Окружная скорость u=r ·ω, тогда

N _т = М _т·ω = ρ Q _т (c_u2 u ₂-c_u1 u₁) (116)

N _т = р _т·Q_т (117) Приравнивая правые части уравнений (116) и (117), получим

р _т = ρ (c_u2 u ₂-c_u1 u₁). (118)

Это уравнение было получено членом Петербургской академии наук Л. Эйлером и носит его имя.

Уравнение Эйлера (118) определяет величину полного приращения давления (теоретически полной удельной объемной работы), сообщенного лопатками колеса 1м³ текучего.

11.3. Составляющие полного давления рабочего колеса

Уравнение Бернулли (111) показывает, что полная энергия потока состоит из статической и скоростной составляющих давления. Установим их соотношения в полном давлении.

Представим, что канал между лопатками перекрыт при вращении колеса с окружной скоростью и. Давление на перекрывающую пластину, определяемое центробежной силой составит (энергия торможения)

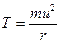, где т масса текучего, кг, r –радиус, м.

Или, переходя к объемным величинам, 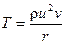. Cчитаем объем единичным (v=1) и произведем замену и =ω r. Элементарная работа центробежной силы окажется 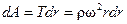или работа на пути от r ₁ до r ₂ 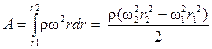. Тогда работа центробежной силы (для 1м³ текучего) создает статическое давление

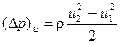. (119)

Теперь представим, что колесо не вращается, но через его межлопаточные каналы проходит текучее с относительной скоростью w. При входе на лопатку полная энергия составит

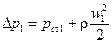, (120)

а на выходе

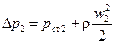, (121)
где р _ст1 и р _ст2 - статические давления у входа и выхода колеса.

Из уравнения (1) Δ р ₁ = Δ р ₂, откуда можно сделать вывод

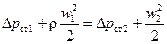и

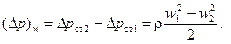(122)

Таким образом, суммарное статическое давление обусловленное наличием центробежной силы и приращения давления вследствие снижения относительной скорости потока на выходе колеса

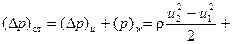
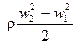. (123)

Полное давление представляет собой разность давлений на выходе и входе в колесо и определяется разностью абсолютных скоростей. Эти скорости с ₁ и с ₂. Подставив их значения в уравнение Бернулли для 1м³ текучего, можно получить на входе и выходе соответственно

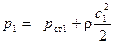и ,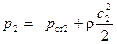

где р _ст1, р _ст2 - статические давления до входа и после выхода из колеса.

Разность давлений представляет собой скоростную составляющую полного давления

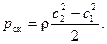
Полное теоретическое давление, развиваемое рабочим колесом, составит

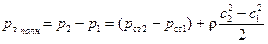. (124)

Таким образом, полное теоретическое давление определяемое тремя факторами, имеет вид

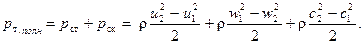(125)

11.4. Схема движения потока в рабочем колесе осевой машины.

Понятие о циркуляции

Под циркуляцией понимается движение по выделенному в потоке замкнутому контуру. Такое движение представлено на рис. 34. Если на замкнутом контуре выделить эле мент длины dl, вектор скорости на котором w, направленный по отношению к касательной под углом α, то циркуляция определяется, как 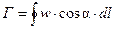, т.е. проекция вектора скорости на тангенциальное направление. Частным случаем является циркуляционное движение по замкнутому круговому контуру радиуса r. Для такого контура циркуляция определяется выражением

Г = 2π ru_r, (126)

где u_r = ω r.

Также показано, что, если в контуре действуют более одного возбудителя (ротора или вихря), то результирующая циркуляция равна сумме циркуляций, возбуждаемых от каждого ротора или вихря

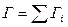. (127)

Рабочее колесо осевых компрессоров представляет собой ротор с лопатками крыловидного профиля.

Крыло представляет собой хорошо обтекаемое ассиметричное тело, имеющее закругленную переднюю и заостренную заднюю кромки. Одна сторона профиля выпуклая, а другая - плоская или слабо вогнутая (рис35). Кратчайшее расстояние между передней и задней кромками называется хордой крыла b. Угол между хордой и направлением движения крыла (скоростью невозмущенного потока) называется углом атаки α.

При обтекании потоком верхней части профиля происходит сужение потока и повышение скорости. Давление в точке 2 оказывается ниже давления в точке 1. Эта разница давлений и есть физическая причина появления подъемной силы крыла.

Н.Е. Жуковский предложил исследовать процесс обтекания потоком профиля крыла суммой двух составляющих (рис.36): плоскопараллельным потоком с обеих сторон и потоком циркуляции, который на верхней стороне суммируется с плоскопараллельным потоком, увеличивая скорость, а на нижней плоской стороне – вычитается, уменьшая скорость.

Это позволило вывести формулу вычисления подъемной силы крыла R_y по оси у, как реакцию на обтекание его потоком с плотностью ρ и имеющего скорость невозмущенного движения потока w_∞.

R_y = ρ w_∞ l Г, (128)

где l - длина крыла.

Подъемная сила направлена перпендикулярно направлению движения невозмущенного потока (рис.3).

В реальных средах при расчетах используются выражения по определению подъемной силы крыла R_y площадью s = b·l и силы его лобового сопротивления R_x по оси х, как

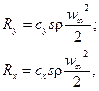(129)

где с_у и с_х – коэффициенты подъемной силы и силы лобового сопротивления, получаемые экспериментально при продувках крыльев в аэродинамических трубах, в функции угла атаки α. Соотношение

с_у / с_х называется качеством крыла, значения которого обычно находится в пределах 50 -70.

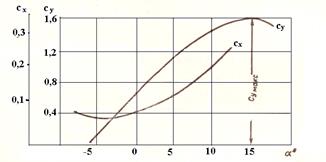
Рис.37. Коэффициенты с_у и с_х в функции угла

атаки α.

Коэффициент подъемной силы зависит от угла атаки. Эта зависимость обычно представляется в виде графика, пример которого приведен на рис.37. Видно, что при увеличении угла атаки подъемная сила растет, что свидетельствует о росте циркуляции вокруг колеса. Подъемная сила достигает максимального значения при углах атаки примерно 13-15⁰, после чего происходит резкое снижение подъемной силы. При значительных отрицательных углах атаки подъемная сила может быть также отрицательной.

Рабочее колесо осевого компрессора представляет собой ротор с расположенными на нем лопаткми-лопостями (рис.38а). Развернутая на плоскость поверхность колеса представляется решеткой лопастей крыловидного профиля. Приуроченная к произвольному радиусу r решетка лопастей показана на рис.38б. На этой решетке линии АВ и СD образуют передний и задний фронты u, а перпендикулярное направление (АD) и (ВС) называются осью решетки a. Лопасти на поверхности ротора располагаются с малым шагом t относительно друг друга, что оказывает влияние на потоки газа в межлопастном пространстве.

При работе колеса решетка лопастей перемещается с окружной скоростью u = ωr.

Абсолютная скорость потока является геометрической суммой относительной w и окружной u составляющих. В идеальном колесе поток в межлопастном канале считается струйным. При обтекании потоком возникает циркуляционный поток вокруг лопасти снижаюший скорость плоско-параллельного потока на передней стороне и увеличивающий – на задней стороне лопасти.

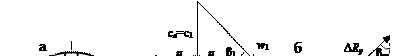План скоростей при обтекании крыла потоком приведен на рис.38б. Здесь с ₁ и с ₂ – соответственно векторы абсолютной скорости потока при входе на лопатку и выходе из нее; с _а – вектор осевой скорости; w ₁ и w ₂ – векторы относительной скорости на входе и выходе; u – окружная скорость на внешнем диаметре колеса; с_u2 – проекция вектора абсолютной скорости при выходе на направление окружной скорости; β₁ и β₂ - соответственно углы между направлениями относительных и окружных скоростей.

Полагая, что поток до входа в рабочее колесо не закручен, поток будет поступать в осевом направлении с ₁= с_а, а вектор относительной скорости w ₁ составит геометрическую разность абсолютной с₁ и окружной и скоростей. Стекая по касательной с лопасти колеса под углом β₂ к фронту решетки с относительной скоростью w ₂, поток получает закрутку с_u2.

Совместим планы скоростей на входе и выходе колеса, как показано на рис.38в, Полученная средняя геометрическая относительная скорость w_т, направленная к фронту решетки под углом β _т, принимается за скорость невозмущенного потока в межлопастном канале рабочего колеса.

11.5 Теоретическая подача рабочего колеса

турбокомпрессора

Теоретическая подача, представляющая количество текучего через колесо в единицу времени, равна произведению площади истечения на скорость, направленную перпендикулярно этой площади.

Для внешнего диаметра D ₂центробежного колеса

Q _т = k _cπ D ₂ b ₂ c_{r 2}, (130)

где k _c – коэффициент стеснения потока, учитывающий толщину лопаток на диаметре D ₂; b ₂ – ширина лопатки; c_{r 2} – радиальная составляющая абсолютной скорости потока.

Для осевого колеса расход определяется по выражению

Q _т = 0,785(D ₂²- D ₁²) c_а. (131)

11.6. Теоретическое давление рабочего колеса

Теоретическое колесо получает от рабочего вала мощность N _т = М _тω и передает ее без потерь потоку N _т = р _т Q _т.

Выделим на осевом рабочем колесе компрессора кольцевой участок длиной Δ r, находящийся на радиусе r (рис.38а). Через этот кольцевой канал площадью s =2π r Δ r проходит текучее со скоростью с_а. Тогда можно записать Δ М _тω = 2π r Δ r·с_а Δр т, откуда

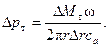(132)

Теоретический момент на этом участке определяется, как произведение подъемной силы R_y на радиус r (рис.38б). Подъемная сила на участке крыла длиной Δ r и скоростью потока w_т направлена под углом β _т к фронту решетки. На основании выражения (128), подъемная сила запишется в виде R_y = ρ w_т Δ r Г.

Проекция вектора подъемной силы на фронтальное направление R_u = ρ w_т Δ r Г· sin β _т, но из плана скоростей (рис.38в) видно, что w_т · sin β _т = с_а. Тогда R_u = ρ с_а Δ r Г, а теоретический момент

Δ М _т = R_u·r = ρ с_аr Δ r Г. (133)

Подставим (133) в (132) и получим выражение теоретического давления рабочего колеса компрессора

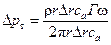или после сокращения в окончательном виде

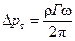, (134)

где на основании (126) Г полная циркуляция вокруг колеса, содержащего z лопастей или лопаток.

При определении циркуляции Г рассмотрим контур АВСD на рис.38б, охватывающий все лопасти рабочего колеса. Суммарная циркуляция Г _АВСDA = Г _АВ+ Г _ВС+ Г _СD+ Г _DA. В месте разрыва колеса Г _ВС= - Г _DA и в сумме равны нулю, т.к. фактически, такого разрыва не существует. Циркуляция по круговому контуру АВ, где движение выбрано против направления вращения колеса (вход в колесо), составит Г _АВ = -2π rс_и1. Циркуляция по круговому контуру СD (выход из колеса), где движение происходит в направлении вращения колеса, составит Г _СD= 2π rс_и2. Суммарная циркуляция вокруг рабочего колеса

Г =2π r (с_и2 - с_и1). (135)

Подставляя (135) в (134) получим

р _т = ρ и (с_и2 - с_и1). (136)

При сравнении формулы (136) с (118) видно, что они полностью аналогичны.

11.7. Теоретические характеристики лопастных

компрессоров

Основной характеристикой лопастных турбомашин является зависимость развиваемого давления от подаваемого во внешнюю сеть количества газа, т.е.

P = f (Q).

При определении вида характеристик будем считать, что на рабочее колесо поток поступает без предварительного закручивания, поэтому проекция вектора абсолютной скорости на окружную с_и1 =0.

В этом случае выражение (136) для полного давления (полной удельной работы) представляется в виде

р _т = ρ ис_и2. (137) При бесконечном числе лопастей относительная скорость w_2∞ направлена по касательной к выходной кромке (рис.39).

При конечном числе лопаток или лопастей рабочего колеса имеет место отклонение потока газа на выходе из колеса. Это отклонение потока, определяемое наложением потока циркуляции на плоскопараллельный поток на выходе из колеса, направлено в сторону противоположную направлению вращения. При этом меняется направление вектора относительной скорости w ₂ при неизменной окружной скорости и, а также снижение значения вектора с_и2 закручивания потока. Это приводит к уменьшению теоретического давления развиваемого колесом. Соотношение

с_и2/с_и2 называется коэффициентом циркуляции k _ц. Значения k _ц = с_и2 / с_и2∞ для разных конструкций колес могут находиться в пределах 0,7-0,9.

Закручивание потока на выходе центробежного колеса, выраженное через расход (Рис.39) с_{и 2} = и ₂ – с_{r 2} ctgβ₂, из выражения (130) 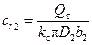. Тогда .

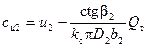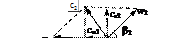
Подставим последнее выражение в (137), а также учтем наличия коэффициента циркуляции р _т = k _ц· р _т∞ и получим

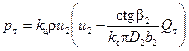(138)

Аналогично, для осевого колеса 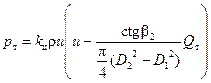. (139)

Видно, что теоретические характеристики p _т= f (Q _т) компрессорных рабочих колес представляются прямыми линиями, наклон которых зависит от направления изгиба лопастей относительно направления их движения, т.е. от угла β₂. На рис.39 приведены схемы варианты изгиба лопаток центробежного колеса.

При лопатках колеса, отогнутых назад угол β₂ < π/2, при радиальных лопатках β₂ = π/2, при лопатках, отогнутых вперед угол

β₂ > π/2. Поэтому для этих колес теоретические характеристики будут иметь вид, приведенный на рис.40.

Значение угла β₂ определяется необходимостью получения большей статической составляющей или большей скоростной составляющей в полном давлении, развиваемым рабочим колесом.

Полное давление, в соответствии с уравнением Эйлера (136) р _{т полн} = ρ и (с_и2 - с_и1).

Скоростная составляющая

.

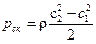Представим значения абсолютных скоростей в проекциях

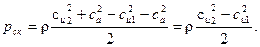
Статическая составляющая, как разность между полным давлением и скоростной составляющей

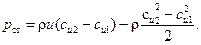
Вынесем за скобку значение полного давления и разделим на него обе части равенства.

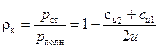. (140)

Полученный коэффициент ρ_к, отражающий содержание статической составляющей в полном давлении, носит название степень реактивности рабочего колеса.

При радиальном входе потока на рабочее колесо проекция с_и1 =0 и выражение (139) принимает вид

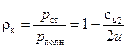. (141)

При угле β₂ < π/2 (Рис.40) статическая составляющая, т.е. повышение давления, оказывается наибольшим, поскольку соотношение с_и2/ и ₂ < 1, деленное на 2 (141) – меньше 0,5, а вычтенное из единицы показывает, что ρ_к, как содержание статической составляющей в полном давлении, больше половины, а в компрессорных установках может принимать значения от 1 до 0,5.

При угле β₂ = π/2 развиваемое давление делится поровну: половина статическая составляющая и половина – скоростная, ρ_к = 0,5.

При загнутых вперед лопатках, угол β₂ > π/2, основная часть приращения энергии приходится на долю скоростной составляющей, что приводит к большим потерям в проточной части и снижению эффективности работы колеса, а кроме того, проявляются неблагоприятные акустические качества. Такие колеса используются лишь в маломощных компрессорах, а ρ_к может принимать значения от 0,5 до 0.

12. ДЕЙСТВИТЕЛЬНЫЕ ИНДИВИДУАЛЬНЫЕ

ХАРАКТЕРИСТИКИ ЛОПАСТНЫХ КОЛЕС КОМПРЕССОРОВ

Действительные индивидуальные характеристики представляются зависимостями P=f(Q), η = f(Q), N = f(Q).

Не вся удельная работа турбомашины может быть использована для транспортирования текучего.

В реальной машине, в отличие от теоретической, имеются потери. Различают потери гидравлические, объемные и механические.

Гидравлические потери складываются из потерь на трение, диффузорные и ударные. Потери на трение пропорциональны квадрату скорости Δ р _тр = k _тqQ². Диффузорные потери при изменении площади сечения канала, обусловленные главным образом преобразованием скоростной составляющей в статическую, также пропорциональные квадрату скорости Δ р _диф = k _диф Q ².

Ударные потери появляются при изменении направления вектора относительной скорости в полости рабочего колеса.

Рассмотрим процесс входа потока на колесо. При радиальном входе потока на колесо проекция с _u1 =0. Значение абсолютной скорости с ₁ на входе определяется, как отношение расхода Q ₁ к площади сечения межлопастных каналов.

На рис.41. показано, что при некоторой производительности Q ₁ и известной окружной скорости и ₁, вектор относительной скорости w ₁ направлен по касательной к входной поверхности лопасти. Это обеспечивает плавность входа потока на колесо, а значит, отсутствие потерь на удар. К такой производительности приурочено номинальное значение расхода через колесо.

При уменьшении подачи Q ₁' < Q ₁, и сохранении величины окружной скорости и ₁, вектор абсолютной скорости уменьшается по величине до с ₁' < c ₁. При этом вектор относительной скорости изменяет свое значение как по величине, так и по направлению w ₁'. Проекция этого вектора на окружную скорость w _{1 и} ' направлена на переднюю поверхность лопасти. Ударяясь о лопасть поток меняет направление движения, т.е. появляется удар. На задней стороне лопасти появится завихрение потока, причиной которого станет отслоение потока от задней кромки.

При увеличении расхода Q ₁'' > Q ₁ проекция вектора относительной скорости w ₁'' на окружную скорость w _{1 и} '', которая направлена в сторону задней стороны лопатки, где также будет изменение направления вектора относительной скорости и связанный с этим удар, сопровождаемый вихреобразованием на передней стороне лопасти.

Ударные явления проявляются тем больше, чем действительная подача отличается от номинальной. Потери на удары и вихреобразование характеризуются выражением Δр = k_уд(Q –Q_н)².

Учет потерь в турбомашине приводит к искажению теоретической характеристики, делая ее нелинейной.

Объемные потери представляют собой утечки, основными из которых являются утечки через зазор на стороне всаса. Потери производительности в устройстве уравновешивания осевого давления при определении объемного КПД не учитываются.

Дата добавления: 2015-06-27