Гидродинамическое подобие

Полученное в предыдущем параграфе число Рейнольдса имеет большое значение в гидравлике, а также в аэродинамике, так как является одним из основных критериев гидродинамического подо­бия. Гидродинамическое подобие — это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кине­матическое и динамическое.

Геометрическое подобие, как известно из геометрии, означает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подоби­ем мы будем понимать подобие тех поверхностей, которые ограни­чивают потоки жидкостей, т. е. подобие русел (рис. 40).

Кинематическое подобие — это подобие линий тока и пропорциональность сходственных скоростей. Очевидно, что для кинематического подобия потоков требуется геометрическое подо­бие русел.

Динамическое подобие означает пропорциональность сил, действующих на сходственные элементы кинематически подоб­ных потоков и равенство углов, характеризующих направление этих сил.

В потоках жидкостей обычно действуют разные силы — давле­ния, вязкости (трения), тяжести и др. Соблюдение пропорциональ­ности всех этих разнородных сил означает так называемое полное гидродинамическое подобие.

Например, пропорциональность сил давления Р и сил трения Т, действующих на сходственные объемы в потоках / и //, можно написать в виде

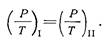
Осуществление на практике полного гидродинамического подо­бия оказывается весьма затруднительным, поэтому обычно имеют дело с частичным (неполным) подобием, при котором наблюдается пропорциональность лишь главных, основных сил. Для напорных те­чений в закрытых руслах, т. е. для потоков в трубах, в гидравли­ческих машинах и т. п., такими главными силами, как показывают расчеты, являются силы давления, трения и их равнодействующие, т. е. силы инерции. Последние, как это можно показать для подоб­ных потоков, пропорциональны произведению динамического давления r u ²/2 на характерную площадь S.

Для геометрически и кинематически подоб­ных потоков и сходственных частиц можно записать:

Для подобных потоков / и // будем иметь

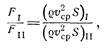
или

Последнее отношение, одинаковое для подобных потоков, назы­вается числом Ньютона и обозначается Ne.

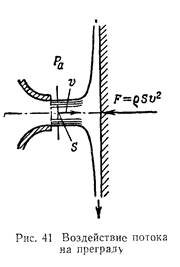
Заметим попутно, что этому же произведению r u ²_ср S в подоб­ных потоках пропорциональны силы, с которыми поток воздей­ствует (или способен воздействовать) на преграды: твердые стенки, лопасти гидромашин, обтекаемые потоком тела и т. п.

Так, например, если поток жидкости наталкивается на безграничную стенку (см. рис. 41), установленную нормально к нему, и в резуль­тате, растекаясь по стенке, меняет свое направление на 90°, то на основании теоремы механики о количестве движения секундный импульс силы равен

Это и есть сила воздействия на преграду. При другом угле уста­новки стенки или другой ее форме и размерах вместо единицы будет другой коэффициент пропорциональности.

Вначале рассмотрим наиболее простой случай — напорное дви­жение идеальной жидкости, т. е. такое движение, при котором отсутствуют силы вязкости, а действие силы тяжести проявляется через давление.

Для этого случая уравнение Бернулли для сечений 1 — 1 и 2—2 (см. рис. 40) имеет следующий вид:

или

Для двух геометрически подобных по­токов правая часть уравнения имеет одно и то же значение: следовательно, левая часть тоже одинакова, т. е. разности давлений пропорциональны динамическим явлениям:

Таким образом, при напорном движении идеальной несжимае­мой жидкости для обеспечения гидродинамического подобия достаточно одного геометрического подобия. Безразмерная величина, представляющая собой отношение разности давлений к динамическому давлению (или разности пьезометрических высот к скорост­ной высоте), называется коэффициентом давления или числом Эйлера и обозначается Еu.

Посмотрим, какому условию должны удовлетворять те же гео­метрически и кинематически подобные потоки, для того чтобы было обеспечено их гидродинамическое подобие при наличии сил вяз­кости, а следовательно, и потерь энергии, т. е. при каком условии числа Ей будут одинаковыми для этих напорных потоков.

Уравнение Бернулли теперь будет иметь следующий вид:

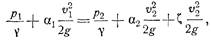
или

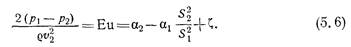
Как видно из уравнения (5.6), числа Еu будут иметь одинако­вые значения для рассматриваемых потоков и потоки будут по­добны друг другу гидродинамически при условии равенства коэф­фициентов сопротивления z, (равенство коэффициентов a₁ и a₂ для сходственных сечений двух потоков следует из их кинематического подобия). Таким образом, коэффициенты z в подобных потоках должны быть одинаковыми, а это значит, что потери напора для сходственных участков (см. рис. 40) пропорциональны скоростным напорам, т. е.

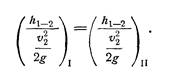
Рассмотрим очень важный в гидравлике случай движения жид­кости — движение с трением в цилиндрической трубе, для кото­рого

Для геометрически подобных потоков отношение l/d одинаково, следовательно, условием гидродинамического подобия в данном случае является одинаковое значение для этих потоков коэффи­циента l. Последний на основании формулы выражается через напряжение трения на стенке t_о и динамическое давление следующим образом:

Следовательно, для двух подобных потоков I и II можно запи­сать

т. е. напряжения трения пропорциональны динамическим давле­ниям.

Условие динамического подобия по­токов:

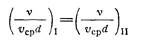
или, переходя к обратным величинам,

В этом заключается закон подобия Рейнольдса, который можно сформулировать следующим образом: для гидродинамиче­ского подобия геометрически подобных потоков с учетом сил вязкости требуется равенство чи­сел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков.

Число Re есть величина, пропорциональная отношению динамиче­ского давления к напряжению трения или, что то же самое, от­ношению сил инерции к силам вязкости. Чем больше скорость и поперечные размеры потока и чем меньше вязкость жидкости, тем больше число Re. Для потока идеальной жидкости число Re бесконечно велико, так как вязкость n=0.

В случаях безнапорных течений под действием разности нивелирных высот вопрос о подобии осложняется, так как приходится вводить еще один критерий подобия — число Фруда, учиты­вающее влияние на движение жидкости силы тяжести. Однако для подавляющего большинства интересующих нас задач в области авиационной техники этот критерий не имеет значения, и мы его рассматривать не будем.

Итак, в подобных потоках, мы имеем равенство безразмерных коэффициентов и чисел a, z, l, Eu, Ne, Re и некоторых других, которые будут введены и рассмотрены ниже. Изменение числа Re означает, что меняется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также меняться. Поэтому все эти коэффициенты в общем случае следует рассматривать как функции числа Re (хотя в некоторых интервалах числа Re они могут оставаться постоянными).

Дата добавления: 2015-06-27