Начальный участок ламинарного течения

Отсюда

ТЕОРИЯ ЛАМИНАРНОГО ТЕЧЕНИЯ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ

ЛАМИНАРНОЕ ТЕЧЕНИЕ

Ламинарное течение является строго упорядоченным слоистым течением без перемешивания жидкости; оно подчиняется закону трения Ньютона и вполне опре­деляется этим законом. Поэтому теория ламинарного течения жид­кости основывается на законе трения Ньютона.

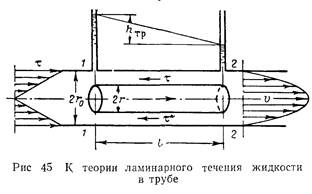
Рассмотрим установившееся ламинарное течение жидкости в прямой круглой цилиндрической трубе с внутренним диаметром d=2r. Чтобы исключить влияние силы тяжести и этим упростить вывод, воспользуемся трубой, расположенной горизонтально. До­статочно далеко от входа в нее выделим отрезок потока длиной l между сечениями 1—1 и 2—2 (рис. 45).

Пусть в первом сечении давление равно p ₁, а во втором p ₂. Ввиду постоянства диаметра трубы скорость и коэффициент a будут неизменными вдоль потока, поэтому уравнение Бернулли для выбранных сечений примет вид

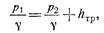
где h _тр—потеря напора на трение.

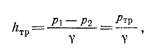
что и показывают пьезометры, установленные в сечениях.

В потоке жидкости выделим цилиндрический объем радиуса r, соосный с трубой и имеющий основания в выбранных сечениях.

Запишем уравнение равномерного движения выделенного объ­ема жидкости в трубе, т. е. равенство нулю суммы двух сил, дей­ствующих на объем: силы давления и силы сопротивления. Обо­значая касательное напряжение на боковой поверхности цилиндра через t, получим

откуда

Из формулы видно, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в функции ра­диуса. Эпюра касательного напряжения показана на том же рис. 45 слева.

Значение скорости на окружности радиуса r таково:

Это есть закон распределения скоростей по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, оказывается параболой второй степени.

Максимальная скорость в центре сечения (при r =0) равна

Входящее в формулу (6. 1) отношение р_тр/l, как видно из рис. 45, представляет собой гидравлический (пьезометрический) уклон, умноженный на g. Эта величина является постоянной вдоль прямой трубы постоянного диаметра.

Для расхода будем иметь:

Найдем среднюю по сечению скорость делением расхода на площадь:

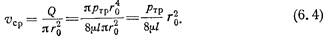
.Сравнивая это выражение с формулой (6.2), приходим к вы­воду, что средняя скорость при ламинарном течении в два раза меньше максимальной, т. е.

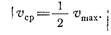
Для получения закона сопротивления, т. е. выражения потери напора на трение h _тр через расход и размеры трубы, определим р _тр из формулы (6. 3):

Разделив уравнение на g, получим потерю напора:

Заменяя m через nr и g через gr, а также переходя от r ₀ к d= 2 r ₀, окончательно получим

Полученный закон сопротивления показывает, что при ламинар­ном течении в круглой трубе потеря напора на трение пропорцио­нальна расходу (скорости) и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, часто называемый законом Пуазейля — Гагена, используется для рас­чета трубопроводов с ламинарным режимом течения.

Закон сопро­тивления:

где

Индекс «л» при l поставлен для того, чтобы подчеркнуть, что здесь речь идет о ламинарном течении.

Следует иметь в виду, что потеря напора на трение при лами­нарном течении пропорциональна скорости в первой степени.

Коэффициент a, учитывающий неравномерность распре­деления скоростей в уравнении Бернулли, для случая стабилизи­рованного ламинарного течения жидкости в круглой трубе:

a = 2.

Итак, истинная кинетическая энергия ламинарного потока с па­раболическим распределением скоростей в два раза превосходит кинетическую энергию того же потока, но при равномерном рас­пределении скоростей.

Таким же образом, можно показать, что секундное количество движения ламинарного потока с параболическим распределением скоростей в b раз больше количества движения того же потока, но при равномерном распределении скоростей, причем коэффициент равен постоянной величине:

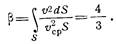
Изложенная теория ламинарного течения жидкости в круглой трубе в общем хорошо подтверждается опытом, и выведенные за­коны сопротивления и распределения скоростей обычно не нуж­даются в каких-либо поправках, за исключением следующих слу­чаев.

1. При течении в начальном участке трубы, где происходит по­степенное установление параболического профиля скоростей. Со­противление на этом участке получается больше, чем на последую­щих участках трубы. Однако это обстоятельство учитывают лишь при расчете очень коротких труб.

2. При течении со значительным теплообменом, т. е. в том слу­чае, когда движение жидкости сопровождается ее нагреванием или охлаждением.

3. При очень высоких перепадах давления.

Если жидкость из какого-либо резервуара входит в прямую трубу постоянного диаметра и движется по ней ламинарным пото­ком, то распределение скоростей вначале получается практически равномерным, особенно если вход выполнен с закруглением (рис. 46). Но затем под действием сил вязкости происходит сле­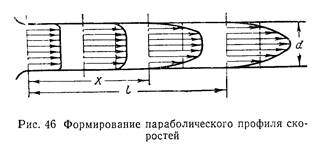 дующее перераспределение скоростей по сечениям: слои жидкости, прилежащие к стенке, тормозятся, а центральная часть потока (ядро), где еще сохраняется равномерное распределение скоростей, движется ускоренно, что обусловлено необходимостью пропустить определенный расход через неизменную площадь. При этом тол­щина слоев заторможенной жидкости постепенно увеличивается, пока не сделается равной радиусу трубы, т. е. пока слои, приле­жащие к противоположным стенкам, не сомкнутся на оси трубы. Только тогда устанавливается характерный для ламинарного тече­ния параболический профиль скоростей.

То расстояние от начала трубы, на котором происходит уста­новление (стабилизация) параболического профиля скоростей, на­зывается начальным участком течения (l _нач). 3а пределами начального участка мы имеем стабилизированное ламинарное течение; параболический профиль скоростей остается неизменным, как бы ни была длинна труба, при условии сохранения ее прямо­линейности и постоянства сечения. Изложенная выше теория ла­минарного течения справедлива именно для этого стабилизирован­ного ламинарного течения и неприменима в пределах начального участка.

Для определения длины начального участка можно пользовать­ся следующей приближенной формулой Шиллера, выражающей эту длину, отнесенную к диаметру трубы, как функцию числа Рейнольдса:

Подставив в формулу Rе_кр=2300, получим максимально возможную длину начального участка, равную 66,5 диаметра.

Как указывалось выше, сопротивление на начальном участке трубы получается больше, чем на последующих участках. Объяс­няется это тем, что значение производной du/dy у стенки трубы на начальном участке больше, чем на участках стабилизированного течения, а потому больше и касательное напряжение, определяемое законом Ньютона, и притом тем больше, чем ближе рассматри­ваемое сечение к началу трубы, т. е. чем меньше координата x.

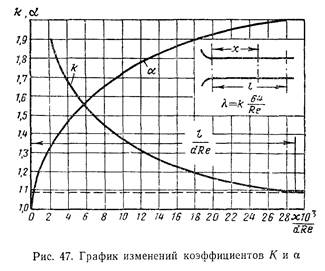
Потеря напора на участке трубы, длина которого l<l_нач, опре­деляется по формулам (6.5) или (6.6) и (6.7), но с поправочным коэффициентом К, большим единицы. Значения этого коэффици­ента могут быть найдены по графику (рис. 47), где коэффициент К изображен как функция безразмерного параметра. С увеличением этого параметра коэффициент К. уменьшается и при

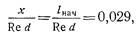
т. е. при х=l _нач, делается равным 1,09. Следовательно, сопротив­ление всего начального участка трубы на 9% больше, чем сопро­тивление такого же участка трубы, взятого в области стабилизи­рованного ламинарного течения.

Для коротких труб значения поправочного коэффициента К, как видно из графика, весьма существенно отличаются от единицы.

В том случае, когда длина трубы больше длины начального участка, потеря напора будет складываться из потери на на­чальном участке и потери на участке стабилизированного тече­ния, т. е.

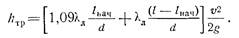
Учитывая формулы (6.7) и (6.8) и выполняя преобразования и подсчет, окончательно получим

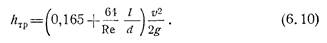
Если относительная длина трубопровода l/d достаточно велика, то дополнительный член в скобках, равный 0,165, можно за ма­лостью отбросить. Но при уточненных расчетах труб, длина кото­рых соизмерима с l _нач, этот член следует учитывать.

Для начального участка трубы с плавным входом a возрастает от 1 до 2 (см. рис. 47).

Дата добавления: 2015-06-27