Гидравлический расчет простых напорных трубопроводов

ТЕХНОЛОГИЧЕСКИЕ РАСЧЕТЫ ТРУБОПРОВОДОВ

При гидравлическом расчете трубопровода обычно решаются три задачи:

- определение диаметра или

- начального давления P₁, или

- пропускной способности Q.

Основные уравнения гидродинамики:

1. Объемный расход:

(4.1)

где ω – линейная скорость, м/с;

S – площадь поперечного сечения трубы, м².

2. Массовый расход:

(4.2)

Для трубопроводов круглого сечения, так как формула (4.1) примет вид

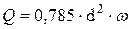(4.3)

3. Уравнение неразрывности: в любой точке трубопровода массовый расход должен быть постоянным – частный случай выражения закона сохранения вещества:

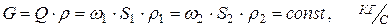(4.4)

Если жидкость несжимаема, то r₁ = r₂ и

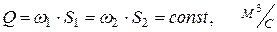(4.5)

то есть это уравнение материального баланса потока.

4. За основу гидравлических расчетов трубопроводов принимается уравнение Бернулли, частный случай выражения закона сохранения энергии, которое для идеальной жидкости имеет вид:

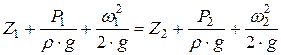(4.6)

где Р₁, Р₂ - давления в сечениях 1 и 2, Па;

ρ - плотность, кг/м³;

ω₁, ω₂, - средние линейные скорости в сечениях 1 и 2, м/с;

g- ускорение свободного падения, м/с².

Каждый член уравнения (4.6) имеет размерность высоты и носит соответствующее название:

Zi - определяет высоту положения различных точек линии тока над плоскостью сравнения, геометрический напор; удельная потенциальная энергия положения.

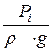, м - называется пьезометрический напор или статический напор; удельная потенциальная энергия давления.

, м - называется динамический или скоростной напор, или удельная кинетическая энергия.

Сумма всех трех напоров определяет запас полной механической энергии потока в соответствующем сечении, отнесенной к единице силы тяжести, и называется полным напором H:

(4.7)

Реальная жидкость обладает вязкостью. В уравнении Бернулли появляется слагаемое, учитывающее потери энергии вследствие гидравлических сопротивлений на участке 1-2:

(4.8)

где h_П – напор на преодоление путевых сопротивлений, то есть на преодоление сил трения и местных сопротивлений трубопроводов.

h_П=h_Т + h_{М ,} (4.9)

где h_Т – потеря напора за счет преодоления сил трения по длине трубопровода;

h_М - потеря напора за счет местных сопротивлений.

При Z₁ =Z₂ и ω₁= ω₂

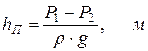(4.10)

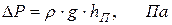(4.11)

Дата добавления: 2015-06-27