
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм симплекс-метода смотри / /
|
|
|
|
Исходные данные примера задачи Таблица 3
| Производ-ственные процессы | Объём работ, га | Часовая Производи-тельность в га агрегатов на базе тракторов | Приведённые затраты руб/га при работе агрегатов на базе тракторов | Объём работы, выполняемый агрегатами на базе тракторов | |||
| Т-150К | МТЗ-80 | Т-150К | МТЗ-80 | Т-150К | МТЗ-80 | ||
| 1.Вспашка | 1,67 | 0,71 | 3,8 | 5,5 | Х11 | Х12 | |
| 2.Посев | 5,0 | 2,5 | 2,7 | 2,5 | Х21 | Х22 | |
| 3.Прика-тывание | 14,8 | 6,67 | 0,5 | 0,5 | Х31 | Х32 |
Пример решения рассматриваемой задачи.
Найти минимум функции
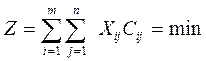
 = 3,8
= 3,8  + 5,5
+ 5,5 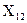 +2,7
+2,7  +2,5
+2,5  +0,5
+0,5  +0,5
+0,5  =min
=min
При условиях
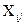
 0 i=1,2,3; j=1,2.
0 i=1,2,3; j=1,2.
1. Суммарная площадь, обрабатываемая агрегатами обоих типов,
 +
+ 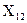 =300;
=300;  +
+  =1000;
=1000;  +
+  =300.
=300.
равна запланированному объёму работ.
2. Величина фонда времени для тракторов Т-150К и МТЗ-80 не должна превышать 300 и 400 часов соответственно.
 +
+ 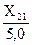 +
+ 
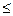 300;
300;  +
+  +
+ 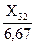
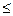 400.
400.
Обратим неравенства системы ограничений в равенства, введя в них дополнительные неизвестные  . Тогда ограничение 3 примет вид:
. Тогда ограничение 3 примет вид:
0,6  + 0,2
+ 0,2  +0,07
+0,07  +
+  =300
=300
1,4 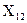 +0,4
+0,4  +0,15
+0,15  +
+ 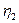 =400
=400
Для отыскания исходного допустимого решения введём вспомогательные неизвестные в первые три уравнения ограничения и приняв неизвестные 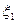 ,
, 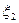 ,
,  и
и  ,
, 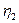 за базисные, выразим их через свободные неизвестные.
за базисные, выразим их через свободные неизвестные.
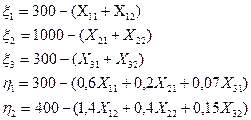
Уравнение вспомогательной функции в данном случае таково
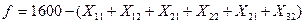
Функция Z унифицированной форме записи примет вид
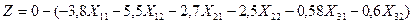
Сводим все коэффициенты перед неизвестными и свободные члены равенства в симплекс-таблицу с тем знаком, какой они имели в унифицированной по форме записи. Все данные располагают в верхних левых углах клеток таблицы.
На первом этапе расчета задача состоит в переводе вспомогательных неизвестных  ,
,  ,
, 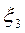 из базисных в свободные.
из базисных в свободные.
Составим опорный план решения задачи по методу минимального элемента,приняв в качестве базисного элемент с наименьшими затратами
 =300 -
=300 - 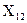 ;
;  =1000-
=1000-  ;
;  =300 -
=300 -  .
.
Подставим в функцию цели и ограничения значения базисных неизвестных и сделаем преобразования
 = 3,8(300 -
= 3,8(300 - 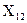 )+ 5,5
)+ 5,5 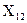 +2,7
+2,7  +2,5(1000-
+2,5(1000-  )+0,5(300 -
)+0,5(300 -  )+0,5
)+0,5 
 = 3790 + 1,7
= 3790 + 1,7 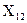 + 0,2
+ 0,2  - 0
- 0  .
.
Опорный план представлен в симплекс –таблице.
| Опорный план Базисные неизвестные | Свободные члены | Свободные неизвестные | Частное | ||
| X12 | X21 | X32 | |||

| |||||

| |||||

| |||||

| -0,6 | 0,2 | -0,07 | ||
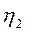
| 1,4 | -0,4 | 0,15 | ||

| -1,7 | -0,2 | -0,1 |
Это решение является также и оптимальным, так как в строке для Z отсутствуют элементы с положительными знаками. Следовательно, дальнейшее уменьшение функции цели невозможно.
Указания к выполнению задания
Для выполнения задания необходимо выбрать исходную информацию из технологических карт, характеризующую производственную ситуацию.
Обозначьте через Xij объёмы работ, выполняемые j-ным агрегатом на i-ом производственном процессе. Для каждого из видов работ напишите ограничение, обозначающее выполнение работ в полном объёме в соответствии с формулой (4).
Определите фонд времени, которым располагают агрегаты каждого типа и напишите ограничения по использованию времени в соответствии с формулой (5).
В соответствии с алгоритмом симплекс-метода выполните указания, содержащиеся в пунктах 1,2,3 и определите величину вспомогательной функции.
Дополнительные и вспомогательные неизвестные примите за базисные и выразите их через свободные.
Уравнения функции цели, вспомогательной функции и уравнения ограничений запишите в унифицированной форме. Сведите все коэффициенты перед неизвестными и свободные члены равенств в общую симплекс-таблицу, располагая все данные в верхних левых углах клеток таблицы со своими знаками. Работа с симплекс-таблицей производится в соответствии с пунктами 8-12 алгоритма симплекс- метода. При достижении допустимого решения (f=0) определите величину неиспользованных ресурсов.
Проверьте является ли допустимое решение оптимальным. Условие оптимальности проверить в соответствии с пунктом 13 алгоритма симплекс-метода. При достижении минимума функции цели выпишите её численное значение и значение требуемых величин.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 677; Нарушение авторских прав?; Мы поможем в написании вашей работы!