Основные положения методики

Условием непрерывности потока является равенство производительностей по всем звеньям комплексов:

n₁W₁ = n₂W₂ = … = n_iW_i = … = n_kW_k , (4.1)

где n_i – число однотипных агрегатов в i-м звене;

W_i – часовая производительность агрегата i-го звена.

Основное звено потока определяет темп всего производственного процесса. Значения W_{i ­} служат исходными данными при определении числа агрегатов в звеньях потока, если количество машин в основном звене известно.

Для системы массового обслуживания типичен случайный поток требований, обладающий свойствами стационарности, ординарности и отсутствием последействия.

Потоки, обладающие этими тремя свойствами, называются простейшими или «пуассоновскими». Для такого потока число требований, попадающих на любой фиксированный интервал времени, будет распределено по закону Пуассона:

, (4.2)

где Р_к(t) – вероятность поступления точно к требований за t время;

t – величина фиксированного интервала времени;

l - параметр потока (математическое ожидание числа требований, поступивших в единицу времени);

lt – параметр закона Пуассона.

Величину l определяют по формуле

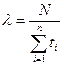, (4.3)

где N – число требований, поступающих от одного агрегата за время

;

t_i – интервал времени между поступлениям i-го и i+1 требованиями.

Характеристикой функционирования обслуживающего звена системы является продолжительность обслуживания одного требования, которая может быть описана показательным законом:

, (4.4)

где F(t) – вероятность того, что время обслуживания не превзойдет заданной величины t;

m - параметр закона (математическое ожидание числа заявок, обслуженных в единицу времени):

, (4.5)

где N₁ – число обслуженных требований;

- общее время обслуживания этих N₁ требований.

Основные показатели системы определяются следующими зависимостями:

- коэффициент простоя обслуживающего агрегата

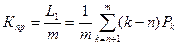, (4.6)

где m, n – число агрегатов в обслуживаемых звеньях;

- средняя длина очереди обслуживаемых агрегатов

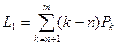; (4.7)

- математическое ожидание числа агрегатов, находящихся в зоне обслуживания

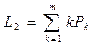; (4.8)

- математическое ожидание числа свободных обслуживающих агрегатов

; (4.9)

- коэффициент простоя обслуживающих агрегатов

(4.10)

Для анализа функционирующей системы необходимо определить вероятность ее пребывания в каждом из возможных состояний. Для систематизации информации расчет ведут в соответствии с табл.4.1.

Дата добавления: 2015-06-27