Алгоритм симплекс-метода

1. Составить математическую модель задачи, т.е. написать функции цели и соответствующие ограничения.

2. Обратить неравенства системы ограничений математической модели в равенства, введя в них дополнительные неизвестные.

3. Для отыскания исходного допустимого решения в уравнения системы ввести вспомогательные неизвестные. Вспомогательные неизвестные не вводят в те уравнения системы, которые содержат дополнительные неизвестные, если каждое из них входит только в одно уравнение системы.

4. Написать уравнение вспомогательной функции

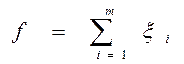
физический смысл которой -недовыполненный объём работы.

5. Приняв дополнительные и вспомогательные неизвестные за базисные, выразить их через свободные.

6. Записать уравнения функции цели, вспомогательной функции и уравнения ограничений в унифицированной форме.

7. Свести все коэффициенты перед неизвестными и свободные члены равенств в общую симплекс-таблицу. Все данные расположить в верхних углах клеток таблицы со своими знаками.

8. Работа с таблицей начинается с выбора генерального элемента при этом руководствуются следующим:

а) найдём в последней строке для функции цели положительный элемент (свободный член не учитывается). Если их нет, то берётся любой, если их несколько, то наименьший.

б) составим отношение свободных членов к элементам выбранного столбца для тех строк, в которых коэффициенты больше нуля и выберем из этих отношений наименьшее. Тогда элемент на пересечении выбранных строки и столбца-генеральный (берётся в рамку). Строка и столбец, на пересечении которых находится генеральный элемент, называются разрешающими;

в) в правый нижний угол клетки с генеральным элементов записывают величину обратную генеральному элементу();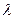

г) умножают на (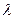) все числа из верхних углов клеток разрешающей строки (кроме клетки с генеральным элементом) и помещают результаты в правые нижние углы этих же клеток;

д) умножают на (- 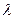) все числа из верхних углов клеток разрешающего столбца и помещают результаты в правые нижние углы этих же клеток;

е) отмечают числа, расположенные в верхних углах разрешающей строки и правых нижних углах разрешающего столбца. Назовём их отмеченными;

ж) правые нижние углы остальных клеток заполняют по следующему правилу: находят отмеченные элементы в строке и столбце, на пересечении которых находится взятая клетка, перемножают их между собой и вносят в правый нижний угол взятой клетки.

Первая таблица заполнена.

9. Свободную неизвестную разрешающего столбца переводят в

базисную разрешающей строки.

10. Элементы, расположенные в правых нижних углах клеток

разрешающей строки и разрешающего столбца первой таблицы,

переносят в левые верхние углы этих же клеток второй таблицы.

11. В левые верхние углы остальных клеток второй таблицы помещают алгебраическую сумму чисел из левого верхнего и правого нижнего угла этой же клетки первой таблицы.

В расшифрованном виде заполненная вторая таблица показывает, как новые базисные неизвестные и линейная форма функции выражены через новые неизвестные.

12. Минимизация вспомогательной функции по симплекс-методу приведет к допустимому решению рассматриваемой системы ограничений. Продолжение симплекс-процесса из допустимого решения приводит к оптимальному.

Если в ходе вычислительной процедуры не удается достичь допустимого решения, что соответствует случаю f>0, то это свидетельствует о несовместимости рассматриваемой системы и об отсутствии оптимального решения, т.е. для выполнения установленного объема работ в заданный срок выделенных ресурсов недостаточно.

13. О достижении искомого оптимального решения свидетельствует наличие только отрицательных элементов в строке симплекс-таблицы для функции цели, если по условию задачи требуется найти ее минимум, или только положительных элементов в соответствующей строке при отыскании максимума функции цели.

Дата добавления: 2015-06-27