Вопросы для оценки качества освоения дисциплины

Тематика самостоятельных и индивидуальных работ

Лабораторные занятия

№ п/п	№ раздела дисциплины	Тематика лабораторных занятий	Трудо-емкость (час.)
		Графический метод решения задачи линейного программирования
		Линейное программирование в среде MS Excel. Оптимальное планирование производства
		Транспортная задача
		Задача о коммивояжере
		Графический метод решения задачи НЛП
		НЛП и оценка риска
		Оптимальное распределение капиталовложений
		Матричной игра как пара двойственных задач линейного программирования.
	1-5	Итоговое тестирование

8. Оценочные средства для текущего контроля успеваемости,
промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов

1. Задача планирования производства

2. Транспортная задача

3.Задача о коммивояжере

4. Графическое решение задачи НЛП. Условная оптимизация.

5. Задача квадратичного программирования.

6. Оптимальное распределение капиталовложений.

7. Матричные игры и методы их решения.

Раздел 1

1. Что такое инструментальные переменные и параметры математической модели? В чем состоит их отличие?

2. Что такое допустимое множество?

3. Что такое критерий оптимизации и целевая функция?

4. Что такое линии уровня целевой функции?

5. Дайте формулировку детерминированной статической задачи оптимизации.

6. Назовите причины неопределенности в параметрах математической модели и объясните ее влияние на решение.

7. Приведите примеры использования математических моделей для описания поведения экономических агентов.

8. Что такое рациональное поведение с точки зрения теории оптимизации?

9. Как методы оптимизации используются при принятии экономических решений?

Раздел 2

10. Сформулируйте задачу линейного программирования.

11. Приведите содержательные примеры задачи линейного программирования.

12. Что такое нормальная (стандартная) и каноническая формы задачи линейного программирования?

13. Какие свойства имеет допустимое множество задачи линейного программирования?

14. Какие свойства имеет оптимальное решение в задаче линейного программирования?

15. Сформулируйте двойственную задачу линейного программирования.

16. Сформулируйте теоремы двойственности в задаче линейного программирования.

17. Дайте интерпретацию двойственных переменных в задаче линейного программирования.

18. Расскажите об анализе чувствительности в задаче линейного программирования.

19. Примените графический метод для решения конкретной задачи линейного программирования.

20. В чем состоят методы решения задач линейного программирования, основанные на направленном переборе вершин (симплекс-метод и др.)?

21. Какие возможности предоставляет среда MS Excel для решения задач линейного программирования?

22. Экономическая и математическая формулировки транспортной задачи. Необходимое и достаточное условия ее разрешимости.

23. Основные способы построения первоначального опорного плана.

24. Потенциалы и их экономический смысл. Метод потенциалов для решения транспортной задачи.

25. Целочисленное линейное программирование. Методы решения задач целочисленного программирования.

26. Постановка задачи о коммивояжере и ее решение методом ветвей и границ.

Раздел 3

27. Сформулируйте общую задачу нелинейного программирования.

28. Сформулируйте необходимое условие локального максимума в общей задаче нелинейного программирования.

29. Что такое функция Лагранжа?

30. Дайте определение седловой точки функции Лагранжа.

31. Сформулируйте и докажите достаточное условие оптимальности с помощью функции Лагранжа.

32. Дайте определение выпуклого множества.

33. Какие свойства имеют выпуклые множества?

34. Дайте определение опорной гиперплоскости.

35. Дайте определение разделяющей гиперплоскости.

36. Сформулируйте понятие выпуклой и вогнутой функций.

37. Что такое строгая выпуклость функции?

38. Сформулируйте достаточное условие выпуклости функции.

39. Какие свойства имеют выпуклые функции?

40. Сформулируйте выпуклую задачу нелинейного программирования.

41. Сформулируйте теорему о глобальном максимуме в выпуклом случае.

42. Приведите содержательный пример выпуклой задачи нелинейного программирования.

43. Сформулируйте теорему Куна-Таккера.

44. Дайте экономическую интерпретацию множителей Лагранжа.

Раздел 4

1. Приведите примеры многошаговых систем в экономике.

45. В чем состоят особенности динамических задач оптимизации?

46. Приведите примеры динамической задачи оптимизации.

47. Что такое многошаговые динамические модели?

48. Что такое непрерывные динамические модели?

49. Что такое управление и переменная состояния в динамических моделях?

50. Приведите примеры задания критерия в динамических задачах оптимизации.

51. В чем состоит метод динамического программирования в многошаговых задачах оптимизации?

52. Сформулируйте принцип оптимальности и запишите уравнение Беллмана.

53. Как задача оптимизации многошаговой системы сводится к задаче математического программирования?

Раздел 5

53. Сформулируйте задачу выбора решений в условиях неопределенности.

54. Основные понятия и определения теории игр. Антагонистические игры. Матричные игры.

55. Матричные игры с седловой точкой. Максиминные и минимаксные стратегии. Смешанные стратегии. Основная теорема теории матричных игр.

56. Игры 2´2, решение в чистых и смешанных стратегиях.

57. Игры 2´n и m´2, графический метод их решения.

58. Доминирование стратегий.

59. Сведение матричной игры паре двойственных задач линейного программирования.

60. Назовите и сформулируйте критерии выбора решений в условиях неопределенности (принцип гарантированного результата, критерий Гурвица, критерий Байеса-Лапласа, критерий Сэвиджа).

61. Как определяется множество допустимых гарантирующих программ?

62. Что такое наилучшая гарантирующая программа?

63. Как используется вероятностная информация о параметрах в задачах принятия решений при случайных параметрах.

64. В чем состоит принятие решений на основе математического ожидания?

65. Как учитывается склонность к риску?

8.3 Примеры тестовых заданий к разделу «Линейное программирование»

1) В каком случае задача линейного программирования (ЛП) в стандартной форме с двумя переменными имеет единственное решение:

а) б)

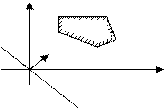x₂ x₂

x₁ x₁

в) x₂

x₁

2) Какой из случаев в задании 1) соответствует множеству решений:

а) из задания 1)

б) из задания 1)

в) из задания 1)

3) В каком случае не существует решения:

а) из задания 1)

б) из задания 1)

в) из задания 1)

4) Случай не существования решения в задании 1) обусловлен:

а) неограниченностью целевой функции;

б) несовместности системы ограничений – неравенств;

в) верно и а) и б).

5) Базисное решение задачи ЛП будет допустимым, если в симплекс – таблице:

а) все свободные члены (кроме строки целевой функции) будут отрицательными;

б) все свободные члены (кроме строки целевой функции) будут положительными;

в) все свободные члены (кроме строки целевой функции) будут неотрицательными;

6) Ограничения в задаче ЛП несовместны, если в симплекс – таблице:

а) в любой строке (кроме строки целевой функции), имеющей отрицательный свободный член, нет ни одного отрицательного элемента;

б) в любой строке (кроме строки целевой функции), имеющей положительный свободный член, все элементы положительны;

в) в любой строке (кроме строки целевой функции), имеющей отрицательный свободный член, все элементы отрицательны.

7) Целевая функция задачи ЛП будет иметь максимальное значение, если в симплекс – таблице:

а) в строке целевой функции все элементы, кроме свободного члена, отрицательны;

б) в строке целевой функции все элементы, кроме свободного члена, положительны;

в) в строке целевой функции все элементы, кроме свободного члена, равны нулю.

8) Полученное оптимальное решение задачи ЛП является альтернативным, если в симплекс-таблице:

а) в строке целевой функции все элементы, кроме свободного члена, одного знака и среди них нет нулевых элементов;

б) в строке целевой функции все элементы, включая свободный член, одного знака и среди них нет нулевых элементов;

в) в строке целевой функции все элементы, кроме свободного члена, одного знака и среди них есть хотя бы один нулевой элемент.

9) Для двойственной задачи, какое из высказываний всегда истинно:

а) число неравенств в системе ограничений одной задачи совпадает с числом ограничений другой задачи;

б) число неравенств в системе ограничений одной задачи совпадает с числом переменных другой задачи;

в) число переменных одной задачи совпадает с числом переменных другой задачи.

10) Какое из высказываний всегда справедливо для оптимальных решений двойственных задач:

а) оптимальные значения целевых функций совпадают;

б) оптимальные значения целевых функций всегда равны нулю;

а) оптимальные значения целевых функций всегда должны различаться.

11) Имеется следующая задача ЛП:

Определить какое решение является оптимальным:

а)

б)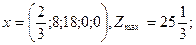

в)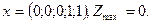

12) Имеется задача ЛП:

z = 2x₁+3x₂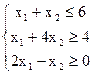

Определить графическим способом, какое решение является оптимальным:

а) x_max = (3; 4); z_max = 18

б) x_max = (2; 4); z_max = 16

в) x_max = (2; 5); z_max = 19

13) Имеется задача ЛП:

z = 2x₁+3x₂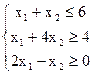

Определить графическим способом, какое решение доставляет min функции z:

а) ;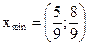

б) ;

в)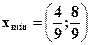

14) Имеется следующая задача ЛП:

z = 2x₁+3x₂ ® max

Решением этой задачи является:

а) x_max = (3; 2);

б) x_max = (6; 4);

в) x_max = (1; 38);

15) Имеется задача ЛП:

z = 3x₁+3x₂ ® max

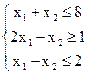
Геометрическим методом установить, какое решение доставляем max:

а) x = (с; 2с), 1≤с≤3;

б) x = (с; 8-с), 3≤с≤6;

в) x = (с; 2с), 3≤с≤6.

16) Имеется задача ЛП:

z = 1+2x₁-3x₂ ® min

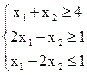
Установить геометрическим способом, что:

а) min достигается в точке х = (1; 3)

б) min достигается в точке х = (1; 1)

в) решение не существует, т.к. F_min = - ∞

17) Имеется задача ЛП:

z = 2x₁-x₂+3x₃-2x₄+x₅ ® min

x_i ≥ 0, i = 1,5

Используя симплекс-метод установить, какое решение является верным:

а) х = (0,5; 1,5; 0; 2; 0)

б) х = (1,5; 0,5; 0; 2; 0)

в) х = (2; 0; 0; 0,5; 1,5)

18) Имеется следующая задача ЛП:

z = -2x₁+x₂ ® max

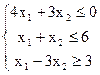
Используя симплекс-метод установить, какой ответ верный:

а) х = (12; 0; 3; 0; 0)

б) х = (3; 0; 12; 3; 0)

в) х = (0; 0; 1; 2; 1)

19) Имеется задача ЛП:

z = -2x₁+x₂ ® min

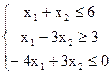
Используя симплекс-метод установить, какой ответ верный:

а) х = (6; 0; 24; 0; 3)

б) х = (24; 0; 0; 6; 3)

в) х = (3; 6; 24; 0; 0)

20) Имеется задача ЛП:

z = 2x₁+3x₂ ® max

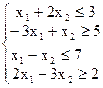
Двойственная задача будет иметь вид:

а) F = 3y₁-6y₂+y₃-y₄ ® max

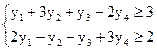
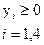
б) F = 2y₁+3y₂

в) F = 3y₁-5y₂+7y₃-2y₄ ® min

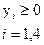
21) Имеется задача ЛП:

F = -x₁+x₂ ® max

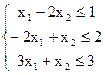
Двойственная задача имеет решение:

а) z_min =

б) z_min =

в) z_min =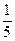

22) Имеется следующее распределение поставок:

а) оно является оптимальным

б) оно не является оптимальным

23) Имеется следующее распределение поставок:

а) оно оптимально

б) оно не оптимально

24) Имеется следующее распределение поставок:

а) оно оптимально

б) оно не оптимально

25) Имеется следующее распределение поставок:

а) оно оптимально

б) оно не оптимально

9. Учебно-методическое и информационное обеспечение учебной дисциплины:

а) основная литература:

1. Абчук В. А. Экономико-математические методы. СПб.: Союз, 1999.

2. Акулич И. Л. Математическое программирование в примерах и задачах. – М.: Высш. шк., 1986.

3. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб. Пособие. – М.:Финансы и статистика, 2005.

4. Благодатских В.И. Введение в оптимальное управление. М.: Высшая школа, 2001.

5. Габасов Р., Кириллова Ф.М. Методы оптимизации. Минск: Изд. БГУ, 1975.

6. Васильев Ф.П. Методы оптимизации. М.: Издательство «Факториал», 2001.

7. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. М.: Высшая школа, 2001.

8. Исследование операций в экономике: Учебное пособие для вузов / Н.Ш. Кремер. – М.: ЮНИТИ, 2004.

9. Костевич Л.С. Математическое программирование: Информационные технологии оптимальных решений: Учебное пособие. – М.: Новое знание, 2003.

10. Просветов Г.И. Математические модели в экономике: учебно-методическое пособие. – М.: РДЛ, 2005.

11. Экономико-математические методы: Учебное пособие/ Ширяев В. Д., Куляшова Н. М., И.А.Карпюк и др. – Саранск: Изд-во Мордов. ун-та, 2009. – 240 с.

б) дополнительная литература

12. Абрамов Л. М., Капустин В. Ф. Математическое программирование. Л.: Изд-во Ленингр. ун-та, 1981.

13. Браверман Э. М. Математические модели планирования и управления в экономических системах. М.: Наука, 1976.

14. Дюбин Г. Н., Суздаль В. Г. Введение в прикладную теорию игр. М.: Наука, 1981. 336 с.

15. Калихман И. Л., Войтенко М. А. Динамическое программирование в примерах и задачах.. М.: Высш. шк., 1979. 125 с.

16. Кундышева Е.С. Математическое моделирование в экономике: учебное пособие. – М.: Дашков и К, 2005. – 352 с.

17. Хазанова Л.Э. Математические методы в экономике. Учебное пособие. М.: Изд. БЕК, 2002.

18. Юдин Д. В., Гольштейн Е. П. Задачи и методы линейного программирования. М.: Сов. радио, 1964. 736 с.

Дата добавления: 2015-06-27