Метод искусственного базиса

Пусть решаем ЗЛП в виде

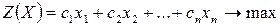
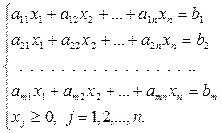
В этом случае общая схема симплекс-метода претерпевает некоторые изменения. А именно:

1) Пусть дан базис некоторого опорного решения и соответствующая ему симплекс-таблица. В верхней строке этой таблицы (заголовки столбцов) располагаются свободные переменные, в крайнем левом столбце – базисные переменные; крайний правый столбец – это столбец свободных членов, а самая нижняя строка является строкой целевой функции и называется вектором относительных оценок. Остальное содержимое таблицы - столбцы матрицы ограничений, отвечающие соответствующим столбцам свободных переменных. Координаты вектора относительных оценок находят по правилу: вектор из коэффициентов при базисных переменных в целевой функции скалярно умножить на i -й столбец симплекс-таблицы и вычесть из найденного числа коэффициент целевой функции при соответствующем свободном переменном.

2) Если все относительные оценки (нижняя строка этой таблицы) неотрицательны, то построено оптимальное опорное решение.

3) Если существует отрицательная оценка и соответствующий ей столбец (разрешающий) состоит из неположительных элементов, то имеет место неразрешимость целевой функции Z (X), то есть max  Z (X) ®+¥.

4) Иначе, выбрать ведущий элемент (задаёт ведущую строку) и сделать с ним шаг жордановых исключений, перейдя к новой симплекс-таблице, которую проанализировать как в пункте 2).

Метод искусственного базиса

Метод искусственного базиса применяется для решения задач ЛП в случае, когда задача не имеет начального опорного решения с базисом из единичных векторов.

Пусть задана задача ЛП в канонической форме, то есть имеет вид (2.1.1), и в ней отсутствует единичный базис. К этой задаче строим вспомогательную задачу (ВЗ):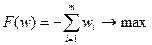

Здесь w ₁, w ₂,…, w_m – искусственные переменные. Запишем ограничения в векторном виде: A ₁ x ₁+ A ₂ x ₂+…+ A_nx_n + A_{n +1} w ₁+…+ A_n+mw_m = B, где , , 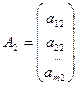…, , , 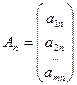, 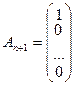…, , 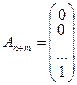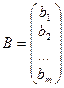. Таким образом, вектора 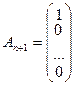, , …, 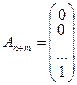образуют единичный базис в R ^m, и все искусственные переменные соответствующие этим векторам будут базисными. Далее строится обычная симплекс-таблица. Если ВЗ не имеет решения в силу неограниченности целевой функции, то исходная задача также не имеет решения по той же причине. Пусть в результате знакомых по симплекс-методу необходимых преобразований получили оптимальную симплекс-таблицу к ВЗ. Очевидно, что максимальное значение целевой функции ВЗ равно 0, то есть max F =0. Если же max F <0, то исходная задача ЛП не имеет решения в силу несовместности системы ограничений. Предположим, что max F =0. Тогда возможны такие ситуации:

1) все искусственные переменные стали свободными и были исключены из таблицы. В этом случае вычеркиваем столбцы, соответствующие искусственным переменным и последнюю строку. Вместо неё приписываем новую строку оценок, но с использованием исходной целевой функции Z (X). Тем самым получена начальная симплекс-таблица для исходной задачи ЛП, к которой применяем симплекс-метод;

2) в оптимальном решении ВЗ хотя бы одна искусственная переменная осталась базисной. Тогда:

а) либо все числа в строках, соответствующих оставшимся базисным искусственным переменным, равны 0;

б) либо есть хоть одно отличное от 0.

В первом случае, поступаем также как и пункте 1). Во втором, выбираем любой ненулевой элемент в качестве ведущего и делаем шаг жордановых исключений. Через конечное число шагов мы придем или к пункту 1), или к пункту 2)а).

Заметим, что если среди векторов A_j, j =1,2,…, n, были вектора, которые могли бы войти в базис, то искусственные переменные вводят только в те уравнения системы ограничений, в которых отсутствует базисная переменная.

Пример. Максимизировать функцию Z = x ₁+2 x ₂-2 x ₃ при ограничениях

Решение. Преобразуем исходную задачу линейного программирования к канонической (см. (2.1.1). Для этого введём в ограничения дополнительные неотрицательные переменные. А именно, в первое неравенство – переменную x ₄ со знаком «+», во второе – x ₅ со знаком «-» (см. §2.2). Система ограничений примет вид:

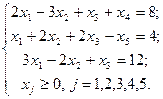
Эту систему запишем в векторной форме: A ₁ x ₁+ A ₂ x ₂+ A ₃ x ₃+ A ₄ x ₄+ A ₅ x ₅= B, где

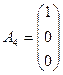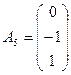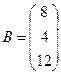, , , , , . Очевидно, что в данной системе ограничений отсутствует единичный базис. Это означает, что среди векторов A_j нет трёх необходимых единичных векторов, которые должны образовывать базис в R ³. Однако заметим, что вектор A ₄ является частью базиса. Ему соответствует базисная переменная x ₄. Необходимо найти ещё два единичных вектора. Для этого применим метод искусственного базиса. Введём искусственные переменные в те уравнения ограничений, в которых не присутствует базисная переменная x ₄ и построим следующую вспомогательную задачу (ВЗ):

F =- w ₁- w ₂®max

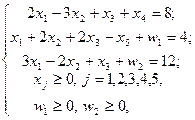
где w ₁, w ₂ – искусственные переменные. Система ограничений ВЗ в векторном виде имеет вид: A ₁ x ₁+ A ₂ x ₂+ A ₃ x ₃+ A ₄ x ₄+ A ₅ x ₅+ A ₆ w ₁+ A ₇ w ₂= B, где вектора A_j, j =1,2,3,4,5 определяются также, как и выше, а и 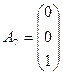. Таким образом, вектора A ₄, A ₆, A ₇ образуют базис в R ³ и им соответствуют базисные переменные (БП) – x ₄, w ₁, w ₂. Все остальные переменные, а именно x ₁, x ₂, x ₃, x ₅ объявляются свободными (СП). Далее к ВЗ применяем обычный симплекс-метод. Как и раньше, см. §5.1, начальный опорный план получается, если присвоить свободным переменным значения, равные нулю. При этом базисные переменные принимают значения, равные числам в соответствующей строке столбца свободных коэффициентов В, то есть x ₁= x ₂= x ₃= x ₅=0¸ а x ₄=8, w ₁=4, w ₂=12. Строим симплекс-таблицу, соответствующую начальному опорному плану:

СП БП .	x1	x2	x 3	x 5	B
x4		-3
w 1				-1
w 2		-2
F	-4		-3		-16

С этой таблицей проводим необходимые преобразования (см. §5.1) симплекс-метода, пока не получим оптимальную симплекс-таблицу или не получим неразрешимость. В нашем случае, мы уже на втором шаге будем иметь такую симплекс-таблицу:

СП БП .	w 1	x2	x 3	w 2	B
x4	-0,5	-3	-0,5	-0,5
x1	0,25		0,75	0,25
x 5	-0,75	-2
F

Эта таблица будет оптимальной для ВЗ. При этом все искусственные переменные стали свободными и max F =0. Вычеркивая столбцы, соответствующие искусственным переменным и последнюю строку, и приписывая новую строку оценок с использованием исходной целевой функции Z (X), получим начальную симплекс-таблицу для исходной задачи ЛП:

СП БП .	x2	x 3	B
x4	-3	-0,5
x1		0,75
x 5	-2
Z	-2	2,75

Проанализировав последнюю таблицу, делаем вывод, что исходная задача ЛП не имеет решения в силу неограниченности целевой функции.

Пример. Минимизировать функцию 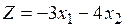при ограничениях

Если ввести дополнительные неотрицательные переменные 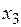, , 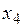, , и перейти к задаче на нахождение максимума целевой функции, исходная задача примет вид:

Z ₁=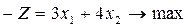

(5.2.1)

По виду ограничений (5.2.1) следует, что очевидного базисного допустимого решения нет. Для порождения базисного допустимого решения применим метод искусственного базиса. Изменим первые два ограничения (два других не создают проблем) введением в левую часть искусственных переменных w ₁ и w ₂ (w ₁, w ₂ ³ 0). Решаем ВЗ:

F =- w ₁- w ₂®max

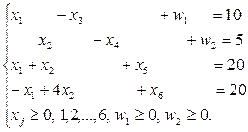
(5.2.2)

Базисное решение (допустимый план) будет иметь вид: , а , , 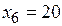w ₁=10, w ₂=5. Строим симплекс-таблицу к ВЗ, соответствующую начальному опорному плану:

СП БП .	x1	x2	x 3	x 4	B
w 1			-1
w 2				-1
x5
x6	-1
F	-1	-1			-15

Проводя преобразования по методу Жордана-Гаусса, на втором шаге будем иметь оптимальную симплекс-таблицу ВЗ (5.2.2). Вычеркивая столбцы, соответствующие искусственным переменным и последнюю строку, и приписывая новую строку оценок с использованием целевой функции Z ₁(X), получим начальную симплекс-таблицу для задачи (5.2.1):

СП БП .	x3	x 4	B
x1	-1
x2		-1
x 5
x 6	-1
Z 1	-3	-4

Преобразования по методу Жордана-Гаусса с последней таблицей приведены ниже:

СП БП .	x3	x 4	B		СП БП .	x3	x 6	B
x1	-1				x1	-1
x2		-1		Þ	x2	-1/4	1/4	30/4	Þ
x 5		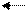			x 5	5/4	-1/4	10/4
x 6	-1				x 4	-1/4	1/4	10/4
Z 1	-3	-4			Z 1	-4

СП БП .	x5	x 6	B
x1	4/5	-1/5
x2	1/5	1/5
x 3	4/5	-1/5
x 4	1/5	1/5
Z 1	16/5	1/5

Все оценки стали положительными, и, следовательно, 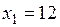, , 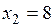, , 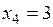x ₅= x ₆=0. Так как и 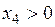, то ограничения, в которые эти переменные входят, превращаются в строгие неравенства. При этом, Z_1max=Z ₁(12;8;2;3;0;0) = 68, а Z_min= -Z_1max=- 68.

Дата добавления: 2015-06-27