Вырожденное базисное решение

Если на каком-либо шаге наибольшее возможное значение переменной (оценочное отношение) достигается в нескольких уравнениях одновременно, то разрешающим можно выбрать любое из этих уравнений. На следующем шаге получится вырожденное базисное решение (одна из базисных переменных равна нулю), а переход к очередному базисному решению может не изменить значения целевой функции.

Пример 4. Пусть в предыдущем примере 3 запас лука равен 30 кг. Тогда на первом шаге решения симплексным методом получим одинаковые оценочные отношения для переменной х₁ в первом и третьем уравнениях.

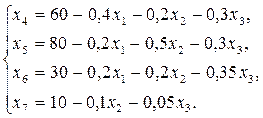(1.16)

Переведем переменную х₁ в базис вместо переменной х₄. Выражая х₁ из первого уравнения и подставляя в остальные уравнения, получим:

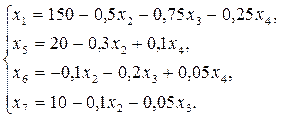(1.17)

Целевая функция примет вид: 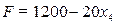. Найденное решение X=(150, 0, 0, 0, 20, 0, 10) является оптимальным и вырожденным: базисная переменная x₆ равна нулю. Хотя свободные переменные х₂ и х₃ входят в выражение целевой функции с нулевыми коэффициентами, увеличить их до какого-либо положительного значения нельзя, т.к. их увеличение приведет к недопустимому (отрицательному) значению переменной x₆.

Однако формально переход к новому базису выполнить можно. Например, переведем в базис переменную х₂ вместо переменной x₆. Тогда получаем систему (1.18), определяющую ещё одно вырожденное базисное решение:

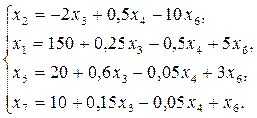(1.18)

Целевая функция остается такой же: 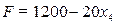. Найденное решение X=(150, 0, 0, 0, 20, 0, 10) является оптимальным и вырожденным: базисная переменная x₂ равна нулю.

Аналогично можно было перевести в базис переменную х₃ и получить ещё одно вырожденное базисное решение X=(150, 0, 0, 0, 20, 0, 10) с нулевой базисной переменной х₃. Различие между этими вырожденными решениями формальное.

Дата добавления: 2015-06-27