
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Экономическая интерпретация двойственной задачи
|
|
|
|
Варианты задач для самостоятельного решения
Варианты задач для самостоятельного решения
Метод искусственного базиса (М-метод)
Варианты задач для самостоятельного решения
Составить экономико-математические модели задач, найти оптимальные решения. Условия задач 11-15 отличаются незначительно, однако это приводит к совершенно различным результатам. Рекомендуется найти решения всех задач и проанализировать их.
Задача 11.
Рацион питания должен содержать не менее 12 единиц питательного вещества В1, не менее 12 единиц питательного вещества В2 и не менее 15 единиц питательного вещества В3. В рацион включены 2 продукта: А1 и А2. Удельное содержание питательных веществ в 1 кг и стоимость 1 кг продуктов заданы в таблице 10. Какое количество каждого продукта нужно включить в рацион для минимизации его стоимости?
Таблица 10. Исходные данные
| продукт | Питательные вещества усл.ед./кг | Стоимость, ден.ед./кг | ||
| В1 | В2 | В3 | ||
| А1 | ||||
| А2 | 1,5 |
(Ответ: минимум целевой функции  . Количество продукта А1 равно
. Количество продукта А1 равно  , количество продукта А2 равно
, количество продукта А2 равно  , где
, где  . Или
. Или  , где
, где  ).
).
Задача 12.
Рацион питания должен содержать не более 12 единиц питательного вещества В1, не менее 12 единиц питательного вещества В2 и не менее 15 единиц питательного вещества В3. В рацион включены 2 продукта: А1 и А2. Удельное содержание питательных веществ в 1 кг и калорийность 1 кг продуктов заданы в таблице 11. Какое количество каждого продукта нужно включить в рацион для его максимальной калорийности?
Таблица 11. Исходные данные
| продукт | Питательные вещества усл.ед./кг | Калорийность, ккал/кг | ||
| В1 | В2 | В3 | ||
| А1 | ||||
| А2 | 1,5 |
(Ответ: максимум целевой функции  . Количество продукта А1 равно
. Количество продукта А1 равно  , количество продукта А2 равно
, количество продукта А2 равно  , где
, где 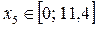 . Или
. Или  , где
, где  ).
).
Задача 13.
Рацион питания должен содержать не менее 12 единиц питательного вещества В1, не более 12 единиц питательного вещества В2 и не менее 15 единиц питательного вещества В3. В рацион включены 2 продукта: А1 и А2. Удельное содержание питательных веществ в 1 кг и калорийность 1 кг продуктов заданы в таблице 12.
Таблица 12. Исходные данные
| продукт | Питательные вещества усл.ед./кг | Калорийность, ккал/кг | ||
| В1 | В2 | В3 | ||
| А1 | ||||
| А2 | 1,5 |
Какое количество каждого продукта нужно включить в рацион для его максимальной калорийности?
(Ответ: максимум целевой функции 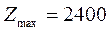 . Количество продукта А1 равно
. Количество продукта А1 равно  , количество продукта А2 равно
, количество продукта А2 равно 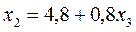 , где
, где  . Или
. Или  , где
, где  ).
).
Задача 14.
Рацион питания должен содержать не менее 12 единиц питательного вещества В1, не менее 12 единиц питательного вещества В2 и не более 15 единиц питательного вещества В3. В рацион включены 2 продукта: А1 и А2. Удельное содержание питательных веществ в 1 кг и калорийность 1 кг продуктов заданы в таблице 13. Какое количество каждого продукта нужно включить в рацион для его максимальной калорийности?
Таблица 13. Исходные данные
| продукт | Питательные вещества усл.ед./кг | Калорийность, ккал/кг | ||
| В1 | В2 | В3 | ||
| А1 | ||||
| А2 | 1,5 |
(Ответ: максимум целевой функции  . Количество продукта А1 равно
. Количество продукта А1 равно 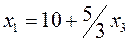 , количество продукта А2 равно
, количество продукта А2 равно  , где
, где  . Или
. Или  , где
, где  ).
).
Задача 15.
Рацион питания должен содержать не менее 12 единиц питательного вещества В1, не менее 9 единиц питательного вещества В2 и не менее 15 единиц питательного вещества В3. В рацион включены 2 продукта: А1 и А2.
Таблица 14. Исходные данные
| продукт | Питательные вещества усл.ед./кг | Стоимость, ден.ед./кг | ||
| В1 | В2 | В3 | ||
| А1 | ||||
| А2 | 1,5 |
Удельное содержание питательных веществ в 1 кг и стоимость 1 кг продуктов заданы в таблице 14. Какое количество каждого продукта нужно включить в рацион для минимизации его стоимости?
(Ответ: минимум целевой функции  . Количество продукта А1 равно
. Количество продукта А1 равно  , количество продукта А2 равно
, количество продукта А2 равно  , решение является вырожденным).
, решение является вырожденным).
Чтобы избежать затруднений при нахождении первоначального базисного решения, применяют метод искусственного базиса. Напомним алгоритм этого метода:
1. Привести ЗЛП к каноническому виду.
2. Построить М-задачу. Для этого в каждое уравнение системы ограничений, не имеющее переменной, исключенной из других уравнений, необходимо ввести искусственную переменную с коэффициентом 1, не меняя знака равенства. Искусственные переменные также вводятся в целевую функцию с коэффициентом –М (если решается задача на максимум) или +М (если решается задача на минимум), где М – сколь угодно большое число.
3. Выписать исходное базисное решение.
4. Решить М-задачу симплексным методом. При решении учесть следующие возможные случаи:
а) если в оптимальном решении М-задачи все искусственные переменные равны 0, то соответствующее решение исходной задачи является оптимальным и экстремумы целевых функций равны;
б) если в оптимальном решении М-задачи хотя бы одна из искусственных переменных не равна 0, то исходная задача не имеет оптимального решения из-за несовместимости системы ограничений;
в) если М-задача не имеет оптимального решения, то исходная задача также не имеет оптимального решения.
Если в процессе решения искусственная переменная выводится из базиса, то можно исключить ее из дальнейших расчетов.
Пример 6. Из бруса длиной 3 м нарезаются заготовки длиной 1м, 1,2м и 2м. Из одного бруса можно нарезать заготовки различными вариантами. При каждом варианте могут оставаться концевые остатки. За смену требуется нарезать 125 заготовок длиной 1м, 10 заготовок длиной 1,2м, 50 заготовок длиной 2м. Определить, какое количество бруса необходимо нарезать по различным вариантам, чтобы выполнить план по нарезке заготовок, и чтобы при этом общая длина концевых остатков была минимальной.
Решение. Определим варианты нарезки бруса и запишем данные в таблицу 15. Составим математическую модель.
Таблица 15. Исходные данные
| Варианты | Количество заготовок заданной длины | Остаток (м) | ||
| 1 м | 1,2 м | 2 м | ||
| 0,8 | ||||
| 0,6 | ||||
| план |
Пусть xi – количество бруса, нарезаемого по варианту i. Найти значения переменных x1, x2, x3, x4, для которых функция  принимает наименьшее значение при ограничениях:
принимает наименьшее значение при ограничениях:
 (1.25)
(1.25)
Задача дана в каноническом виде. Составим М-задачу, для этого введем в первое уравнение переменную х5, во второе – переменную х6, в третье – переменную х7, в целевую функцию добавим М х5 + М х6+ М х7.
 (1.26)
(1.26)
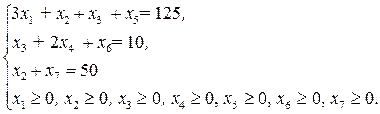 (1.27)
(1.27)
Решаем задачу симплексным методом. Начальный базис х5, х6, х7.
 (1.28)
(1.28)
 (1.29)
(1.29)
Решение допустимое  . Переведем в базис переменную х 2, входящую в целевую функцию с отрицательным коэффициентом. Оценочные отношения для переменной х2 равны 125 и 50. Третье уравнение системы является разрешающим. Новый базис х2, х6, х7. Т.к. искусственная переменная х7 выведена из базиса, не учитываем ее в дальнейших вычислениях. Система ограничений и целевая функция имеют вид:
. Переведем в базис переменную х 2, входящую в целевую функцию с отрицательным коэффициентом. Оценочные отношения для переменной х2 равны 125 и 50. Третье уравнение системы является разрешающим. Новый базис х2, х6, х7. Т.к. искусственная переменная х7 выведена из базиса, не учитываем ее в дальнейших вычислениях. Система ограничений и целевая функция имеют вид:
 (1.30)
(1.30)
 . (1.31)
. (1.31)
Решение 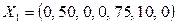 . Переведем в базис переменную х1, выражая её из второго уравнения. Новый базис x1, х2, х6. Т.к. переменная х5 выведена из базиса, исключаем ее из дальнейшего решения.
. Переведем в базис переменную х1, выражая её из второго уравнения. Новый базис x1, х2, х6. Т.к. переменная х5 выведена из базиса, исключаем ее из дальнейшего решения.
 (1.32)
(1.32)
 . (1.33)
. (1.33)
Решение  . Т.к. M может быть сколь угодно большим числом, то коэффициенты при переменных x3, x4 отрицательны, и решение пока не является оптимальным. Переведем в базис переменную x4, выразив её из третьего уравнения. Новый базис x1, х2, х4. Т.к. переменная х6 выведена из базиса, исключаем ее из дальнейшего решения. Система ограничений и целевая функция принимают вид:
. Т.к. M может быть сколь угодно большим числом, то коэффициенты при переменных x3, x4 отрицательны, и решение пока не является оптимальным. Переведем в базис переменную x4, выразив её из третьего уравнения. Новый базис x1, х2, х4. Т.к. переменная х6 выведена из базиса, исключаем ее из дальнейшего решения. Система ограничений и целевая функция принимают вид:
 (1.34)
(1.34)
 . (1.35)
. (1.35)
Выполнен критерий оптимальности решения задачи на минимум целевой функции. Оптимальное решение  , минимальное значение целевой функции
, минимальное значение целевой функции  .
.
Ответ: X = (25, 50, 0, 5), общая длина концевых остатков 3 м.
Составить экономико-математические модели задач, найти оптимальные решения методом искусственного базиса.
Задача 16.
Рацион питания должен содержать 10 единиц питательного вещества В1, не менее 12 единиц питательного вещества В2 и не менее 15 единиц питательного вещества В3. В рацион включены 2 продукта: А1 и А2. Удельное содержание питательных веществ в 1 кг и стоимость 1 кг продуктов заданы в таблице 16. Какое количество каждого продукта нужно включить в рацион для минимизации его стоимости?
Таблица 16. Исходные данные
| продукт | Питательные вещества усл.ед./кг | Стоимость, ден.ед./кг | ||
| В1 | В2 | В3 | ||
| А1 | ||||
| А2 | 1,5 |
(Ответ: минимум целевой функции  . Количество продукта А1 равно
. Количество продукта А1 равно  кг, количество продукта А2 равно
кг, количество продукта А2 равно  кг).
кг).
Задача 17.
Рацион питания должен содержать 10 единиц питательного вещества В1, не более 12 единиц питательного вещества В2 и не более 15 единиц питательного вещества В3. В рацион включены 2 продукта: А1 и А2. Удельное содержание питательных веществ в 1 кг и калорийность 1 кг продуктов заданы в таблице 17. Какое количество каждого продукта нужно включить в рацион для его максимальной калорийности?
Таблица 17. Исходные данные
| продукт | Питательные вещества усл.ед./кг | калорийность, ккал/кг | ||
| В1 | В2 | В3 | ||
| А1 | ||||
| А2 | 1,5 | 2,5 |
(Ответ:  ,
,  кг,
кг,  кг).
кг).
Задача 18.
Рацион питания должен содержать 12 единиц питательного вещества В1 и 10 единиц питательного вещества В2. В рацион включены 3 продукта: А1, А2, А3. Удельное содержание питательных веществ в 1 кг и стоимость 1 кг продуктов заданы в таблице 18. Какое количество каждого продукта нужно включить в рацион для минимизации его стоимости?
Таблица 18. Исходные данные
| продукт | Питательные вещества усл.ед./кг | Стоимость, ден.ед./кг | |
| В1 | В2 | ||
| А1 | |||
| А2 | |||
| А3 |
(Ответ: минимум целевой функции  ,
,  кг,
кг,  кг).
кг).
Задача 19.
Рацион питания должен содержать 12 единиц питательного вещества В1 и 10 единиц питательного вещества В2. В рацион включены 3 продукта: А1, А2, А3. Удельное содержание питательных веществ в 1 кг и стоимость 1 кг продуктов заданы в таблице 19. Какое количество каждого продукта нужно включить в рацион для минимизации его стоимости?
Таблица 19. Исходные данные
| продукт | Питательные вещества усл.ед./кг | Стоимость, ден.ед./кг | |
| В1 | В2 | ||
| А1 | |||
| А2 | |||
| А3 |
(Ответ: минимум целевой функции  . Количество продукта А1 равно
. Количество продукта А1 равно  кг, количество продукта А3 равно
кг, количество продукта А3 равно  кг).
кг).
Задача 20.
Рацион питания должен содержать 12 единиц питательного вещества В1 и 10 единиц питательного вещества В2. В рацион включены 4 продукта: А1, А2, А3 и А4. Удельное содержание питательных веществ в 1 кг и стоимость 1 кг продуктов заданы в таблице 20.
Таблица 20. Исходные данные
| продукт | Питательные вещества усл.ед./кг | Стоимость, ден.ед./кг | |
| В1 | В2 | ||
| А1 | |||
| А2 | |||
| А3 | |||
| А4 |
Какое количество каждого продукта нужно включить в рацион для минимизации его стоимости?
(Ответ: минимум целевой функции  . Количество продукта А1 равно
. Количество продукта А1 равно  кг, количество продукта А4 равно
кг, количество продукта А4 равно  кг).
кг).
2. Двойственные задачи
Каждой задаче линейного программирования соответствует другая задача, называемая двойственной, или сопряженной по отношению к исходной. Понятие двойственности взаимно. Теория двойственности позволяет провести полезные качественные исследования задач линейного программирования. В зависимости от вида исходной задачи различают симметричную, несимметричную и смешанные пары двойственных задач.
Напомним правила составления двойственных задач. Таблицы соответствия исходных и двойственных задач рекомендуется посмотреть в учебном пособии (курсе лекций) «Методы оптимальных решений)
Симметричная пара
1. В исходной задаче знаки неравенств системы m ограничений приводятся к единому виду: «≤» в задаче на максимум и «≥» в задаче на минимум.
2. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная yi, i =1, 2, … m.
3. Составляется целевая функция Z от переменных yi (i =1, 2, … m), коэффициентами которой будут свободные члены системы ограничений исходной задачи. Цель меняется на противоположную.
4. Составляется система ограничений двойственной задачи. Матрицу коэффициентов системы ограничений двойственной задачи получают транспонированием матрицы коэффициентов исходной задачи. Знаки неравенств системы ограничений двойственной задачи противоположны знакам неравенств в исходной задаче. Свободными членами неравенств системы ограничений являются коэффициенты целевой функции исходной задачи. Переменные yi (i =1, 2, … m) неотрицательны.
Пример 7. Исходная задача (см. математическую модель примера 2): Найти значения переменных х1, х2, удовлетворяющие условиям:
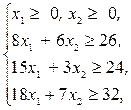 (2.1)
(2.1)
при которых целевая функция  принимает минимальное значение.
принимает минимальное значение.
Составим двойственную задачу.
Найти значения переменных y1, y2, y3, удовлетворяющие условиям
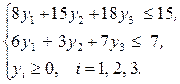 (2.2)
(2.2)
для которых функция  принимает наибольшее значение.
принимает наибольшее значение.
Несимметричная пара
1. Если система ограничений исходной задачи состоит из уравнений, то соответствующие им двойственные переменные произвольны по знаку.
2. Если переменные xj (j=1, 2, …n) исходной задачи неотрицательны, то ограничения двойственной задачи имеют вид неравенств со знаком «≤» для задачи на максимум и «≥» для задачи на минимум.
3. Далее построение двойственной задачи выполняется как для симметричной пары.
Пример 8. Исходная задача (см. математическую модель примера 6): найти значения переменных x1, x2, x3, x4, для которых функция  принимает наименьшее значение при ограничениях:
принимает наименьшее значение при ограничениях:
 (2.3)
(2.3)
Составим двойственную задачу.
Найти значения переменных y1, y2, y3, удовлетворяющие условиям
 (2.4)
(2.4)
для которых функция  принимает наибольшее значение.
принимает наибольшее значение.
Смешанная пара
1. Если система ограничений исходной задачи содержит как уравнения, так и неравенства, то при построении двойственной задачи придерживаются следующего правила. Если двойственная переменная поставлена в соответствие ограничению-неравенству, то она неотрицательна, если уравнению, то переменная произвольна по знаку.
2. Если переменная исходной задачи неотрицательна, то ей ставится в соответствие ограничение–неравенство, если переменная произвольна по знаку, то соответствующее ей ограничение является уравнением.
3. Далее построение двойственной задачи выполняется как для симметричной пары.
Задача 21.
Составить двойственные задачи для задач 1 – 5, решить одну из составленных задач.
Задача 22.
Составить двойственные задачи для задач 6 – 10, решить одну из составленных задач.
Задача 23.
Составить двойственные задачи для задач 11 – 15, решить одну из составленных задач.
Задача 24.
Составить двойственные задачи для задач 16 – 20, решить одну из составленных задач.
Задача 25.
Составить двойственные задачи для примеров 3 – 5, решить одну из составленных задач.
Предположим, что у предприятия есть возможность вместо того, чтобы производить продукцию и реализовывать её по заданным (внешним) ценам, продать сырьё некоторому покупателю по оптимальным для себя (внутренним) ценам. Эти цены предприятие заинтересовано установить такими, чтобы полученная выручка была не менее той суммы, которую можно получить при реализации выпущенной продукции. С другой стороны покупатель заинтересован в том, чтобы затраты на все ресурсы для него были минимальны.
Пример 9. Рассмотрим задачу из примера 1 (см.п.1.1).
Математическая модель исходной задачи: найти значения переменных x1, x2, удовлетворяющие условиям
 , (2.5)
, (2.5)
при которых целевая функция  принимает максимальное значение. В результате решения симплексным методом получено оптимальное значение переменных
принимает максимальное значение. В результате решения симплексным методом получено оптимальное значение переменных 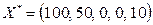 и выражение целевой функции для этого решения
и выражение целевой функции для этого решения  .
.
Составим двойственную задачу. Найти значения переменных y1, y2, y3, удовлетворяющие условиям
 , (2.6)
, (2.6)
при которых целевая функция
 (2.7)
(2.7)
Решение задачи симплексным методом выполнить самостоятельно.
Для взаимно двойственных задач существует соответствие между переменными и решениями. Для рассматриваемого примера это соответствие приведено в таблице 21.
Таблица 21. Соответствие решений взаимно-двойственных задач
| Компоненты оптимального решения исходной задачи | ||||
| Число единиц продукции (первоначальные переменные) | Остатки ресурсов (дополнительные переменные) | |||
| х1 100 | х2 50 | х3 0 | х4 0 | х5 10 |
| у4 0 | у5 0 | у1 500 | у2 250 | у3 0 |
| Превышение затрат на ресурсы над ценой реализации (дополнительные переменные) | Объективно обусловленные оценки ресурсов (первоначальные переменные) | |||
| Компоненты оптимального решения двойственной задачи |
Решения двойственной задачи – абсолютные величины коэффициентов целевой функции F в оптимальном решении прямой задачи ЛП. Переменные у1, у2, у3 и у4 представляют собой объективно обусловленные оценки ресурсов. Они определяют степень дефицитности ресурсов, показывают, на сколько денежных единиц изменится максимальная прибыль от реализации продукции при изменении запаса соответствующего ресурса на 1 единицу. Т.е. в рассмотренном примере при увеличении (уменьшении) запаса ресурса «суфле» на 1 единицу максимальная прибыль увеличится (уменьшится) на 500 руб., а при увеличении (уменьшении) запаса ресурса «взбитые сливки» на 1 единицу максимальная прибыль увеличится (уменьшится) на 250 руб. В оптимальный план производства входят те виды продукции, для которых затраты на ресурсы не превышают цену реализации.
Пример 10. Оценить целесообразность включения в план производства третьего вида десерта, если:
А) на производство 1 кг будет затрачено 0,2 кг суфле, 0,3 кг взбитых сливок и 0,5 кг клубничного джема, а цена реализации равна 200 руб.
Вычислим затраты на ресурсы для производства единицы этой продукции 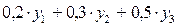 и сравним значение с ценой реализации:
и сравним значение с ценой реализации:  . Следовательно, следует рассмотреть вариант выпуск данной продукции и снова решить задачу оптимизации.
. Следовательно, следует рассмотреть вариант выпуск данной продукции и снова решить задачу оптимизации.
Б) на производство 1 кг будет затрачено 0,35 кг суфле, 0,25 кг взбитых сливок и 0,4 кг клубничного джема, а цена реализации равна 220 руб.
Вычислим затраты на ресурсы для производства единицы этой продукции  и сравним значение с ценой реализации:
и сравним значение с ценой реализации:  . Следовательно, выпуск данной продукции не является целесообразным.
. Следовательно, выпуск данной продукции не является целесообразным.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 1072; Нарушение авторских прав?; Мы поможем в написании вашей работы!