Логических функций методом Квайна

Минимизация логических функций с использованием законов и тождеств

При минимизации получают самую короткую форму записи ЛФ, при которой ЛКС имеет наименьшее число логических элементов. Наиболее часто используются метод Квайна, карты Карно и Вейча.

Метод Квайна. По этомуметоду минимальная форма ЛФ получается с использованием операции склеивания и закона поглощения.

1. Определяется число членов ЛФ, приведённой к канонической форме СДНФ или СКНФ. Число членов функции равно числу столбцов матрицы.

2. Производится сравнение первого члена ЛФ с каждым из последующих. При этом вы-являются пары членов, различающихся тем, что один из аргументов в одном из членов представлен без инверсии, а в другом – с инверсией. Затем производится склеивание та-ких пар членов. Результат склеивания вписываем в матрицу как простые импликанты. Против членов СДНФ (СКНФ), поглощаемых простой импликантой, ставится «+».

3. Выписываются простые импликанты, составляющие ядро ЛФ, и добавляем импликанты, не входящие в ядро, но обеспечивающие перекрытие всех столбцов матрицы.

ПРКТИЧЕСКАЯ РАБОТА № 2

Цель: Получить и отработать первичные навыки минимизации

Задание.

1. По логической функции, заданной в форме таблицы истинности, составить

выражения СДНФ и СКНФ.

2. Минимизировать СДНФ методом Квайна, используя импликантную матрицу

3.По полученной минимальной ДНФ составить логическую схему.

Контрольные вопросы

1. Дать определения СДНФ и СКНФ.

2. Правила составления СДНФ и СКНФ по таблице истинности.

3. Показать применение операции склеивания и закона поглощения.

4. Дать определение базиса, перечислить его варианты.

5. Привести УГО ЛЭ И, НЕ. ИЛИ, И-НЕ, ИЛИ-НЕ.

Содержание отчёта

Тема; цель; таблица истинности; логические выражения СДНФ и СКНФ, состав-

ленные по таблице истинности; преобразования по получению минимальной

ДНФ; минимальная ДНФ; логическая схема, составленная по минимальной ДНФ.

Литература

1. Мизерная З.А. Методическое пособие по цифровой схемотехнике, с. 48, 52-56.

2. Мизерная З.А. Цифровые устройства, микропроцессоры и их программиро-

вание. Альбом схем, Л.14.

( ) ( ) ( )

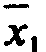
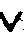
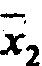
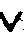
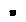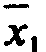
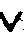
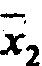
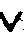
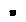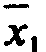
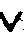
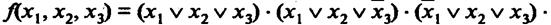
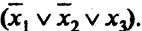
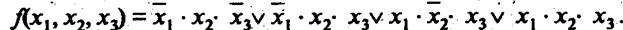
1. Для выполнения операции склеивания в выражении СДНФ попарным сравнением выявляются пары членов, различающихся тем, что один из аргументов в одном из членов представлен без инверсии, а в другом – с инверсией. Затем производится склеивание таких пар членов.

1-й и 2-й члены ( результат склеивания );

2-й и 4-й члены (результат склеивания );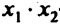

3-й и 4-й члены (результат склеивания ).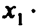

2. Результаты склеивания вводятся в выражение ЛФ в качестве дополнительных членов и далее осуществляется поглощение. Оно основано на равенстве:

= (1+ ) = .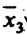

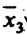Член поглощает те члены исходного выражения, в которых он содержится, а именно 1-й и 2-й, член 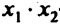поглощает 2-й и 4-й, член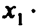 поглощает 3-й и 4-й.

Поглощённые члены

ПР № 2 Минимизация логических функций методом Квайна.

Знать: способы минимизации ЛФ; уметь: синтезировать логические схемы, синтезировать не полностью заданные логические функции.

ПР № 3.Построение логических схем в заданном базисе

Формы представления логических функций

Переход от табличного представления к аналитическому

Минимизация логических функций с использованием законов и тождеств.

Карты Вейча и Карно для двух, трёх, четырёх переменных.

1. Определяется число членов ЛФ, приведённой к канонической форме СДНФ или СКНФ. Число членов функции равно числу столбцов матрицы. (В выражении СДНФ таких членов четыре).

ПРКТИЧЕСКАЯ РАБОТА № 3

ПОСТРОЕНИЕ ЛОГИЧЕСКИХ СХЕМ В ЗАДАННОМ БАЗИСЕ

Цель: Отработать навыки минимизации логических функций методом

Дата добавления: 2015-06-27