Графический метод решения ЗЛП с двумя переменными

Изложим графический метод решения ОЗЛП с двумя переменными на примере задачи оптимального планирования производства продукции.

Задача 1. Для производства компьютерных столов I-го и II-го видов требуются три типа ресурсов: дерево, пластик и трудозатраты. Потребности в ресурсах для производства одного стола каждого вида, запасы ресурсов, а также прибыль от реализации одного стола каждого вида, заданы в следующей таблице 1:

Требуется, решив задачу графическим методом, найти план выпуска продукции, позволяющий получить наибольшую прибыль.

Решение. Если обозначить символом х ₁ выпуск (число единиц) продукции I-го вида, а символом х ₂ выпуск (число единиц) продукции II-го вида, то, в соответствии с таблицей 1., неизвестные х ₁ и х ₂ будут удовлетворять следующей системе ограничений:

(1.3)

По условию задачи необходимо найти оптимальный план производства продукции, т.е. такой план (х ₁, х ₂), который доставляет максимум функции прибыли

Z = 200 х ₁ + 300 х ₂.

Для того чтобы решить поставленную задачу графическим методом, изобразим на координатной плоскости x₁Ox₂ область, заданную системой ограничений (1.3):

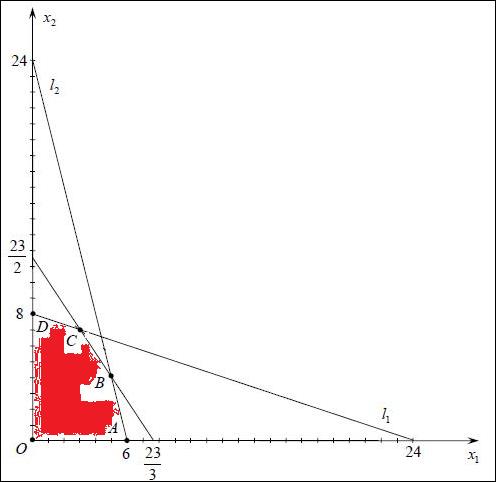Рис.1

Эта область лежит в первом квадранте координатной плоскости, а её граница задается системой уравнений (1.4) в которой каждое уравнение является уравнением прямой линии. Прямая l 1, заданная уравнением { х 1 + 3 х 2 = 24}, проходит через точки (24;0) и (0;8); прямая l 2, заданная уравнением {4 х 1 + х 2 = 24}, проходит через точки (6; 0) и (0; 24); прямая l 3, заданная уравнением {3 х 1 + 2 х 2 = 23}, проходит через точки (23/3;0) и (0;23/2). Таким образом, область, заданная системой (1.3), является пятиугольником OABCD.

Рис.2

Рассмотрим теперь вектор = (2; 3) с началом в точке О (0;0), параллельный вектору (200; 300), и построим линию нулевого уровня прибыли Z = 0, т.е. прямую 200 х 1 + 300 х 2 = 0. Эта прямая проходит через точку О (0;0) и перпендикулярна вектору . Каждая из линий уровня Z = const является прямой, параллельной линии нулевого уровня Z = 0 (рис.2). Будем передвигать линию нулевого уровня Z =0 параллельно самой себе в направлении вектора = (2; 3) до тех пор, пока она пересекается с точками пятиугольника OABCD. Очевидно, что последними точками, в которых передвигаемая линия пересекается с пятиугольником OABCD, могут быть только вершины пятиугольника.

Рис.2

Найдем координаты вершин пятиугольника. Координаты точки В удовлетворяют системе уравнений

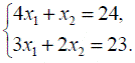
Решая эту систему, находим, что B = (5;4). Координаты точки C удовлетворяют системе уравнений

Решая эту систему уравнений, находим, что C = (3;7). Координаты остальных вершин пятиугольника нам уже известны: A = (6;0), D = (0;8), O = (0;0).

Подсчитаем теперь значения, которые принимает функция прибыли в вершинах пятиугольника:

Z (О) = Z (0; 0) = 200 · 0 + 300 · 0 = 0;

Z (A) = Z (6; 0) = 200 · 6 + 300 · 0 = 1200;

Z (B) = Z (5; 4) = 200 · 5 + 300 · 4 = 2200;

Z (C) = Z (3; 7) = 200 · 3 + 300 · 7 = 2700;

Z (D) = Z (8; 0) = 200 · 8 + 300 · 0 = 1600.

Таким образом, наибольшая прибыль достигается в точке C (3; 7), и оптимальный план имеет вид (х ₁, х ₂) = (3; 7).

Рис.3

Ответ. Наибольшая прибыль 2700 рублей достигается при выпуске 3 компьютерных столов I-го вида и 7 компьютерных столов II-го вида.

Дата добавления: 2015-06-27