Понятие опорного плана

Симплексный метод позволяет улучшать план задачи наиболее рациональным способом, опираясь на критерии оптимальности решения.

Базисным решением ЗЛП называется такое решение системы уравнений (1.6), в котором все свободные переменные равны 0.

Базисное решение ЗЛП называется опорным решением (опорным планом), если в нем все базисные переменные неотрицательны.

В теории симплекс-метода доказывается, что, если максимум целевой функции при данной в ЗЛП системе ограничений существует, то он достигается на опорном решении. Опорное решение, на котором целевая функция достигает максимума, является оптимальным планом.

Замечание. Не следует думать, что ЗЛП всегда имеет решение. Система ограничений, например, может быть противоречивой и задавать пустое множество решений. Система ограничений может также задавать неограниченное множество, на котором функция прибыли является неограниченной.

Для выяснения вопроса: является ли найденный план оптимальным, пользоваться оценками переменных Δ _j, j =1, n, которые вычисляются по формулам

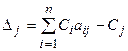(1.9)

Критерии оптимальности решения:

при отыскании максимума функции: если оценки всех переменных неотрицательны, то значение целевой функции максимально и решение оптимально, т.е.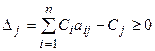

при отыскании минимума функции: если оценки всех переменных неположительные, то значение целевой функции минимально и решение оптимально, т.е. .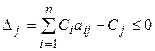

Дата добавления: 2015-06-27