Понятие высказывания. Тема 4.5. Высказывания и операции над ними

Тема 4.5. Высказывания и операции над ними

Цель занятия – изучить первичные понятия логики высказываний, необходимые для построения логически непротиворечивых утверждений относительно оценивания социально-правовых явлений.

Теоретические сведения

Многие элементарные логические задачи можно решить при помощи логики высказываний, которая является основной составной частью математической (символической) логики.

Логика высказываний имеет дело с действиями над нерасчленёнными высказываниями, т. е., в отличие от более сложных частей логики, здесь не интересуются структурой высказывания, тем, каковы его подлежащее и сказуемое, как и чем они соединены, и т. п.

Высказыванием называется любое повествовательное предложение, относительно которого точно известно, что оно истинно или ложно.

Например, высказываниями являются предложения «Москва – столица Российской Федерации», «Медь не является проводником электричества», так как о первом можно сказать, что оно истинно, а о втором, что оно ложно.

Однако не всякое предложение является высказыванием. Например, восклицательные и вопросительные предложения высказываниями не являются («Встать, суд идёт!», «Иди сюда», «Что вменяется в вину подсудимому?», «Который час?» и т.д.). Не являются высказываниями и определения понятий, например, «юридическим лицом признаётся организация, которая имеет в собственности, хозяйственном ведении или оперативном управлении обособленное имущество и отвечает по своим обязательствам этим имуществом, может от своего имени приобретать и осуществлять имущественные и личные неимущественные права, нести обязанности, быть истцом и ответчиком в суде».

Не являются высказываниями и предложения «Он виновен в совершении правонарушения» - в нём не указано, о каком человеке идёт речь или при каких х рассматривают равенство. Однако, предложение «Некоторые люди виновны в совершении правонарушений» уже является высказыванием (истинно).

Если высказывание истинное, то ему предписывается значение «истина» (другие обозначения: «1», «И», «Т»). Ложному высказыванию предписывается значение «ложь» (другие обозначения: «0», «Л», «F»). Совокупность возможных значений высказывания образует множество истинности {0, 1}.

Высказывания могут быть выражены с помощью слов, а также математических, химических и прочих знаков. Приведём примеры:

а) заинтересованное лицо вправе обратиться в суд за защитой своих нарушенных или оспариваемых прав и законных интересов (истинное высказывание);

б) 2 + 3 > 5 (ложное высказывание);

в) в пределах нашей Галактики существуют внеземные цивилизации (это высказывание, несомненно, либо истинно, либо ложно, но пока неизвестно, какая из этих возможностей выполняется).

Рассмотрим три примера.

1. Даны два множества: С = (l; 3) – интервал числовой оси; D = [2; 4] – отрезок числовой оси. Выбрать истинные для них высказывания:

а)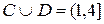

б)

в)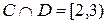

г)

Ответ: а) и в).

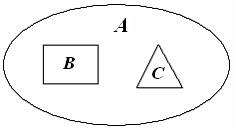2. Множества А, В и С изображены на диаграмме. Выбрать истинные для них высказывания:

а)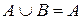

б)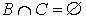

в)

г)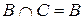

Ответ: а) и б).

3. Даны множества А = { a, b, 4, 5} и В = { b, d, 3, 4}. Выбрать истинные для них высказывания:

а)

б)

в)

г)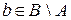

Ответ: а) и б).

Из произвольных высказываний при помощи логических операций можно образовать другие высказывания. Это мы делаем в повседневной жизни, когда объединяем предложения при помощи связок или же отрицаем что-либо, что нам сообщили, и т. п. Например, можно отрицать высказывание «Поезд не уходит в 12 часов» и образовать из этого высказывания, помещённого в кавычки, новое высказывание: «Неправда, что поезд не уходит в 12 часов». Из двух высказываний – «Этот поезд опаздывает» и «Я не могу его дождаться» – можно образовать новое высказывание: «Этот поезд опаздывает, и я не могу его дождаться». Но из тех же двух «простых» высказываний можно образовать и другое «сложное» высказывание, применив союз «если..., то...»: «Если этот поезд опаздывает, то я не могу его дождаться». Из высказываний – «Теперь перед нами зажёгся зелёный сигнал» и «Теперь перед нами зажёгся красный сигнал» – можно образовать высказывание: «Теперь перед нами зажёгся зелёный сигнал», которое исключает (утверждение) «теперь перед нами зажёгся красный сигнал».

Высказывание, которое можно разложить на части, будем называть сложным, а неразложимое далее высказывание - простым (или элементарным).

Например, сложное высказывание «Сегодня в первой половине дня я был в академии, а после обеда пошёл в библиотеку» состоит из двух простых высказываний: «Сегодня в первой половине дня я был в академии» и «Сегодня после обеда я пошёл в библиотеку».

Дата добавления: 2015-06-27