Быстрое начало

Попробуем уменьшить объемы производства красок, например 2 т краски Н и 2 т краски В. Подставив эти числа в таблицу, мы получим новые значения прибыли, суточного расхода продуктов и спроса на краски. Продолжая этот процесс перебора вариантов, мы рано или поздно найдем вариант, при котором прибыль будет максимальной, и в то же время будут выполнены ограничения по запасам продуктов и спросу на краски. Это будет означать, что мы решили оптимизацион­ную задачу.

Однако такой процесс поиска решений может оказаться слишком долгим и утомительным. Кроме того, если бы номенклатура красок включала в себя не два, а, например, десять видов, мы вообще вряд ли смогли бы найти оптимальный вариант организации производства путем простого перебора вариантов.

Таблица 2

изменяемых ячеек и ограничений. В таких случаях на помощь прихо­дят специальные программы — решатели оптимизационных задач. Одна из таких программ — Solver — включена в систему Microsoft Ex­cel как дополнение Поиск решения (раздел меню Сервис).

Поиск решения

Для решения оптимизационной задачи, оформленной в структуре ЭТ, необходимо вызвать приложение Поиск решения (меню Сервис). При этом на экране появится диалоговое окно Поиск решения.

В поле Установить целевую (ячейку) окна Поиск решения необхо­димо ввести имя (адрес) соответствующей ячейки. Для нашего приме­ра это ячейка Е24. Затем указывается вид оптимизации путем «нажа­тия» соответствующей кнопки, расположенной непосредственно под полем целевой ячейки.

В поле Изменяя ячейки указываются имена (адреса) ячеек, содер­жимое которых подбирается программой поиска решения таким обра­зом, чтобы обеспечить требуемое значение целевой ячейки. Для на­шего примера изменяемыми ячейками являются В23, В24, содержа­щие объемы суточного производства красок.

В этом смысле усложнение задачи связано с увеличением ее раз­мерности (количества изменяемых ячеек) и числа ограничений. Прак­тические задачи оптимизации включают в себя десятки и даже сотни

Кнопка Предположить поможет вам в определении изменяемых яче­ек: нажатие этой кнопки приводит к вводу в окно Изменяя ячейки имен тех ячеек, которые программа поиска расценивает как изменяемые.

Часть 1. Поиск решений на электронных таблицах

Быстрое начало

В поле Ограничения должны быть введены все ограничения, свя­занные с решаемой задачей. В нашем примере такие ограничения де­лятся на три группы:

• естественные ограничения: В23:В24 >= 0 (они вводятся путем
нажатия на кнопку Параметры, а затем кнопку Неотрицатель­
ные значения);

• ограничения по запасам исходных продуктов:
E16:E17<=D16:D17;

• ограничения спроса на краски: В23 >= D29; В24 <= СЗО.
Добавление, изменение и удаление ограничений осуществляется с

использованием соответствующих кнопок, расположенных в правой части поля ограничений окна Поиск решения.

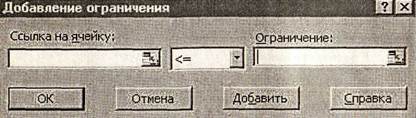
Нажатие кнопки Добавить или Изменить приводит к вызову до­полнительного окна определения ограничений. В поле Ссылка на ячейку вводится левая часть ограничения. Список Ограничение вклю­чает в себя отношение равенства, «больше или равно», «меньше или равно», отношение цел, которое означает, что левая часть ограниче­ния должна быть целым числом, отношение двоич, означающее, что левая часть ограничения должна быть двоичным числом (т. е. прини­мающим значения 0 или 1). При использовании отношений цел и двоич поле справа от списка ограничений остается пустым. При испо­льзовании любого другого отношения в этом поле размещается пра­вая часть ограничения.

Нажатие кнопки Выполнить окна Поиск решения приводит к запу­ску процесса поиска решения задачи оптимизации. В результате по­иска программа находит такие значения изменяемых ячеек, при кото­рых достигается оптимальное значение целевой ячейки.

Для нашей задачи о красках оптимальное решение будет опреде­ляться следующими значениями изменяемых ячеек:

• объем производства краски Н (ячейка В23) — 3,33 т;

• объем производства краски В (ячейка В24) — 1,33 т.
Оптимальное значение целевой ячейки Е24 (при выполнении всех

ограничений) составит 12,65 тыс. долл.

Виды ячеек и зависимости

Выше мы уже использовали понятия изменяемой ячейки и целевой ячейки. Изменяемые ячейки всегда содержат числовую информацию, Которая подбирается в процессе поиска решения таким образом, что­бы обеспечить оптимальное значение целевой ячейки. Кроме того, в процессе поиска используются еще два вида ячеек:

• ячейки исходных данных;

• зависимые ячейки.

Ячейки исходных данных содержат числа, которые не меняются программой поиска решения (Solver), зависимые ячейки содержат формулы, которые неоднократно перевычисляются в процессе поиска решения. Ячейки разного вида в электронной таблице целесообразно закрашивать разным цветом. Например, в приведенных выше табли­цах мы использовали для этого разные степени затушевывания ячеек.

Наличие зависимостей между ячейками разных видов в среде EXCEL может быть проиллюстрировано графом зависимостей, по-строенным непосредственно на структуре таблицы (см. табл. 3). По-строение такого графа связано с использованием меню Сервис (Зави-симости, Панель зависимостей).

Таблица 3

Использование графа зависимостей позволяет формально контро­лировать структуру таблицы. В правильно составленной таблице все стрелки должны начинаться в изменяемых ячейках или ячейках исход-

16

Часть 1. Поиск решений на электронных таблицах

Быстрое начало

17

ных данных и заканчиваться в зависимой или целевой ячейке. Из це­левой ячейки стрелки зависимостей не могут выходить. Таблица счи­тается хорошо структурированной, если граф зависимостей наглядно иллюстрирует причинно-следственные связи между ячейками. «Запу­танный» граф свидетельствует о плохой структуризации таблицы.

Дата добавления: 2015-06-27