
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поиск решения
|
|
|
|
Общие рекомендации по разработке структур электронных таблиц
В общем случае структура ЭТ, ориентированная на решение оптимизационной задачи, может быть представлена в различных видах. Выбор конкретного определяется во многом субъективными представлениями исследователя о наглядности таблицы, удобстве ее использования, уровне детализации и т. п.
Необходимым условием корректной структуры ЭТ, используемой для решения оптимизационной задачи, является наличие изменяемых ячеек и целевой ячейки.
Приведем несколько практических рекомендаций по оформлению задачи в структуре таблицы.
При оформлении оптимизационной задачи в структуре электронных таблиц рекомендуется использовать во всех текстовых ячейках, содержащих названия столбцов и/или строк, определение размерности содержимого ячейки. Например «т» (тонна), или «час», или «долл.» и т. п. Использование размерностей способствует выявлению грубых ошибок, связанных, например, с умножением «столов на стулья» и получением в результате «тонн в минуту».
Просмотрите разработанную структуру ЭТ с использованием графа зависимостей: все стрелки должны быть направлены от изменяемых ячеек и ячеек исходных данных через зависимые ячейки в сторо-
ну целевой. Хорошо структурированная таблица характеризуется на-глядным графом зависимостей.
Все числовые данные задачи должны быть размещены в соответ-ствующих ячейках ЭТ, несмотря на то что использование программы поиска решения позволяет вводить отдельные числовые данные непо-средственно через окно ограничений Поиска решения. Это позволяет при исследовании различных вариантов организации системы изме-нять такие данные, не затрагивая окна поиска.
Старайтесь использовать в ЭТ числа по возможности одного порядка или близких порядков (например, 10 и 100). Это упрощает процесс поиска решения и позволяет избежать многих вычислительных ошибок. Например, в рассмотренной выше задаче о красках оптовая ■на тонны краски выражается в тысячах долларов. Однако в таблице И< пользуются значения 3 (тыс. долл.) и 2 (тыс. долл.), а не 3000 долл. И 2000 долл. Это сделано специально в стиле этой рекомендации.
В процессе разработки ЭТ вы можете столкнуться с ситуацией, когда отдельные ограничения «не вписываются» в структуру таблицы. В этом случае такие ограничения целесообразно оформить в виде ототдельной таблицы, связанной с вашей задачей. В этом стиле оформлена, например, таблица «Ограничения суточного спроса по видам красок» (см. табл. 1).
Использование ЭТ для решения оптимизационной задачи будет Солее наглядным, если вы будете использовать именование ячеек. До-стоинства именования ячеек наглядно проявляются при работе с программой поиска решения, при анализе отчетов по результатам моделирования и при построении сводных таблиц по результатам исследований системы.
Например, мы хотим назвать ячейку В23, в которой сохраняется сугочный объем производства краски для наружных работ, именем Краска_Н, ячейку В24 с аналогичным содержимым — именем Крас-ка_В, а целевую ячейку с общим доходом — именем Общий_доход. Для этого мы последовательно выделяем каждую из этих ячеек в таблице и обращаемся к меню Вставка, раздел Имя, оператор Присвоить, который открывает окно именования. В это окно вводится соответст-вующее имя, и в дальнейшем во всех отчетах поименованная ячейка будет идентифицироваться присвоенным ей именем.
Стиль оформления ограничений
Хорошим стилем оформления задания на поиск решения является использование ограничений, левые и правые части которых состоит только из имени (адреса) одной ячейки или массива ячеек. При этом
20
Часть 1. Поиск решений на электронных таблицах
Поиск решения
21


 все промежуточные вычисления, связанные с определением левой и правой частей таких ограничений, размещаются в зависимых ячейках таблицы. (Последние версии EXCEL не допускают отклонений от этого стиля.) Ниже приведены примеры оформления ограничений.
все промежуточные вычисления, связанные с определением левой и правой частей таких ограничений, размещаются в зависимых ячейках таблицы. (Последние версии EXCEL не допускают отклонений от этого стиля.) Ниже приведены примеры оформления ограничений.
| Плохой стиль | Хороший стиль |
| В2К=С21;В22<=С22; | В21:В22<=С21.С22 |
| Е4>=12; | E4>=G7; (В ячейке G7 размещено число 12) |
| G4+K4=N4; | L7=N4; (В ячейке L7 размещена формула =G4+K4) |
Второй пример иллюстрирует общее правило: все исходные числовые данные целесообразно размещать в ячейках ЭТ, а не вводить в окно ограничений (рекомендация 3 в приведенном выше списке). Это связано с возможностями изменять такие данные в процессе исследования системы.
Ниже приводятся некоторые рекомендации по оформлению ограничений на оптимальное решение задачи.
Старайтесь избегать избыточных ограничений. Тривиальный пример таких ограничений: В23<=16, В23<=20. Избыточные ограничения всегда «мешают» процессу поиска и в некоторых случаях могут привести к зацикливанию вычислений.
Использование ограничений в форме равенства всегда «сужает» полигон для поиска решения. Такие ограничения в общем случае оказываются слишком «жесткими» для реальных задач, и (по возможности) следует отдавать предпочтение более «мягким» неравенствам.
Противоречивые ограничения делают процесс поиска бессмысленным. Тривиальный пример таких ограничений: В24 <= СЗО; В24 >= СЗО+2. Такие ограничения всегда связаны с отсутствием решения задачи. Основная проблема, связанная с противоречивыми ограничениями, заключается в том, что для сложных задач с большим числом ограничений весьма трудно выявить противоречия между отдельными ограничениями.
Проблема начальных значений
Перед вызовом программы поиска решения в изменяемые ячейки целесообразно ввести некоторые ориентировочные начальные значения. В некоторых случаях от выбора таких значений зависит и сама возможность найти оптимальное решение задачи. В этой связи рекомендуется несколько раз вычислить таблицу для различных значений
и пленяемых ячеек и «почувствовать» тенденции приближения к оптимуму. Запомните, чем ближе начальные значения к точке оптимума,
тем легче и быстрее его удается найти. К сожалению, эта рекомендация может быть использована для решения сравнительно простых задач.|
В этом отношении может может оказаться полезным специальное
средство системы EXCEL — Подбор параметра (меню Сервис).
В поле Установить в ячейке указывается адрес (имя) ячейки, содержащей формулу (в нашем случае это целевая ячейка Е24), которая устанавливает зависимость от изменяемой ячейки (в нашем случае ЭТО В23). Подбор параметра позволяет подобрать такое значение изменяемой ячейки, при котором целевая получит установленное нами значение (в этом примере 16).


 Отметим, что подбор параметра ни в коей мере не заменяет поиск решения. Подбор параметра можно рассматривать как простейший вариант такого поиска, когда устанавливается связь только между двумя ячейками без учета каких-либо дополнительных ограничений. Именно поэтому мы рекомендуем использовать подбор параметра лишь, как вспомогательное средство, способное помочь при решении проблемы начальных значений.
Отметим, что подбор параметра ни в коей мере не заменяет поиск решения. Подбор параметра можно рассматривать как простейший вариант такого поиска, когда устанавливается связь только между двумя ячейками без учета каких-либо дополнительных ограничений. Именно поэтому мы рекомендуем использовать подбор параметра лишь, как вспомогательное средство, способное помочь при решении проблемы начальных значений.
Результат работы программы подбора параметра занесется в ячейку, указанную в поле Изменяя значение ячейки (в нашем примере В23).
Управление процессом поиска решения
Нажатие кнопки Выполнить окна Поиск решения приводит к запуску процесса поиска решения задачи оптимизации. При невозможности запустить поиск решения система может вывести следующие сообщения:
Недостаточно памяти для решения задачи. Это означает, что ЕXCEL не смог выделить память для поиска решения. Закройте ненужные файлы или приложения и попытайтесь запустить программу снова.

|
|
Часть 1. Поиск решений на электронных таблицах
В другом сеансе EXCEL используется SOLVER. Запущено несколько сеансов работы с EXCEL, в одном из которых используется SOLVER — программа поиска решения. Попробуйте завершить или закрыть окна, связанные с этими сеансами.
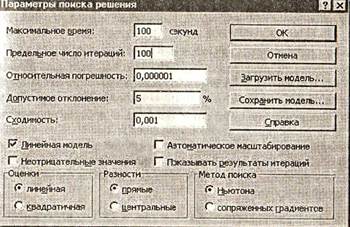
 Управление процессом поиска решения связано с использованием диалогового окна Параметры поиска решения, которое открывается при нажатии кнопки Параметры окна Поиск решения.
Управление процессом поиска решения связано с использованием диалогового окна Параметры поиска решения, которое открывается при нажатии кнопки Параметры окна Поиск решения.
Все параметры, управляющие процессом поиска решения, делятся на три группы, которые описываются ниже. Предварительно заметим, что каждый из этих параметров имеет значение по умолчанию, подходящее для большинства решаемых задач. Использование новых установок параметров обычно необходимо для проведения серьезных исследований сложных систем управления.
Поиск решения

 Группа параметров, определяющих время процесса поиска
Группа параметров, определяющих время процесса поиска
К этой группе относятся четыре параметра: максимальное время, число итераций, точность и допустимое отклонение.
К настройке этих параметров целесообразно обратиться при получении следующих сообщений о неудачном окончании процесса поис-1 ка решения:
• поиск решения не может улучшить текущее решение. Все огра
ничения выполнены;
• остановка при исчерпании лимита времени;
• остановка при выполнении максимального числа итераций.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 388; Нарушение авторских прав?; Мы поможем в написании вашей работы!