Операции над матрицами в аналитической (символьной) форме

Графики матричных и векторных зависимостей.

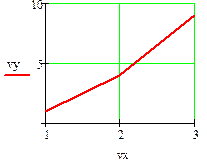В Маткаде возможно построение графиков по данным, записанным в векторной и матричной форме. На рис.15 показано построение двумерного графика по данным векторов vx и vy, а на рис.16. – построение трехмерного графика по заданным в матрице аргументам и вектору функции.

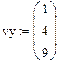
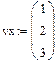
Рис.15. Построение двумерного графика по векторным данным.

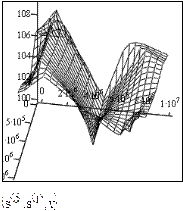Заданы двумерная матрица аргументов S и вектор значений функции этих аргументов Y.Показано построение графика.

.

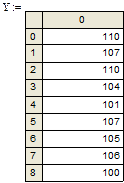
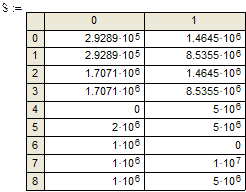
Рис.16.Трехмерный график данных, записанных в векторной форме.

Системы компьютерной алгебры снабжаются специальным процессором для выполнения аналитических (символьных) вычислений. Его основой является ядро, хранящее всю совокупность формул и формульных преобразований, с помощью которых производятся аналитические вычисления. Чем больше этих формул в ядре, тем надежней работа символьного процессора и тем вероятнее, что поставленная задача будет решена, разумеется, если такое решение существует в принципе (что бывает далеко не всегда).

Ядро символьного процессора системы Маткад- несколько упрощенный вариант ядра известной системы символьной математики Maple V фирмы Waterloo Maple Software, у которой MathSoft (разработчик Маткада) приобрела лицензию на его применение, благодаря чему Маткад стал системой символьной математики.

Введение в систему Маткад символьных вычислений придает ей качественно новые возможности. Символьные вычисления выполняются, в конечном счете, столь же просто для пользователя, как, скажем, вычисление квадрата х.

Операции, относящиеся к работе символьного процессора, содержатся в подменю позиции Symbolic (Символика) главного меню.

Чтобы символьные операции выполнялись, процессору необходимо указать, над каким выражением эти операции должны производиться, т е надо выделить выражение. Для ряда операций следует не только указать выражение, к которому они относятся, но и наметить переменную, относительно которой выполняется та или иная символьная операция. Само выражение в таком случае не выделяется, ведь и так ясно, что если маркер ввода выделяет переменную какого-либо выражения, то это выражение уже отмечено наличием в нем выделяемой переменной

Символьные операции разбиты на пять характерных разделов. Это операции с выражениями, операции с переменными, операции с матрицами, операции преобразования, стиль эволюции. Первыми идут наиболее часто используемые операции Они могут выполняться с выражениями, содержащими комплексные числа или имеющими решения в комплексном виде

В данной лабораторной работе мы рассмотрим только операции с матрицами. В дальнейшем будут рассмотрены и другие символьные операции.

Символьный процессор системы Маткад обеспечивает проведение в символьном виде трех наиболее распространенных матричных операций транспонирования и обращения матриц, а также вычисления их детерминанта.

При символьных вычислениях, прежде всего, следует вызвать панель символьных вычислений нажатием кнопки на математической панели.

После этого появится панель символьных вычислений, показанная на рис.17

.

Рис.17. Панель символьных вычислений

Для символьных операций над матрицами нам понадобится только предпоследняя строка этого окна, с помощью кнопок которой и производятся транспонирование, обращение матрицы и нахождение ее определителя.

Задача 10. Используя кнопки панели символьных вычислений, провести аналитическое транспонирование и обращение произвольной матрицы, например:

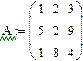
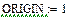
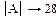
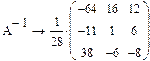
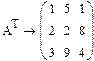
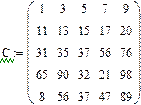
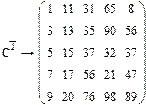
Рис.18. Пример символьного решения матричных задач.

ЛАБОРАТОРНАЯ РАБОТА №4. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ В МАТЕМАТИЧЕСКОМ ПАКЕТЕ «Маткад».

Алгебраические уравнения в Маткаде решаются как численными, так и аналитическими методами. В данной лабораторной работе будут рассмотрены оба метода

Численное решение системы линейных алгебраических уравнений.

При численном решении систем линейных уравнений используется специальный вычислительный блок, открываемый служебным словом - директивой Given. Блок имеет следующую структуру:

Задание начальных приближений

Дата добавления: 2015-06-27