Ограничительные условия выражения с функцией find

Уравнения

Given

Задача 1. Пусть надо решить систему

3x+8y-9z=12

5x-9y+2z=34

8x-6y+5z=98.

Для этого необходимо совершить следующие действия:

1)Набрать начальные приближения – произвольные числа

х:=1 y:=1 z:=1

2).Набрать с клавиатуры директиву given (дано);

3).Набрать систему уравнений, обязательно записывая знак умножения, причем знак = нужно набирать не на арифметической панели, а на панели логики, которая выводится на экран кнопкой математической панели.

4).Набрать выражение otvet:= find(x,y,z)

5). Набрать otvet =

После этого будет получен ответ в виде вектора – столбца.

Вместо слова otvet можно использовать любой набор букв и цифр, начинающийся с буквы. Этот набор обозначает имя, которое Вы присваиваете вектору ответов. На рис.1 показано решение этой системы

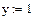
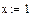
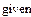
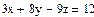
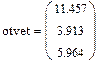
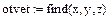
Рис.1. Решение системы линейных уравнений в решающем блоке

Задача 1.. Решите приведенную выше систему.

Задача 2. Решите самостоятельно приведенные ниже системы линейных алгебраических уравнений

А) 5x+6y-9z+2v-7w=90

3x-4y+5z-3v+4w=12

9x+y +3z-2v +9w=51

7x+2y-8z+v +10w=32

6x+5y-4z+3v-2w= 87

Б) 4.5x+7.9y-2.1v+6.75w+7.9u= 43

5.6x+7.2y+9.8z+3.9v+3.4w+8.3u=12.54

5.6x+98.5y+43.7z+67.85v+4.9w+21.5u = 54.98

65.75x+54.32y-78.32z-565.9v+32w+78.54u = 55.5

54.2x+76.45y+32.23z+ 45.71v+43.43w+ u = 65.21

8.9x+9.8y-5.6z+6.5v-4.5w+2.1u = 0

Подобным образом можно решать и нелинейные уравнения. Однако они имеют несколько корней. Задавшись начальными приближениями, мы найдем в лучшем случае один корень, ближайший к начальному приближению. Таким способом имеет смысл искать корни трансцендентных уравнений, имеющие, как известно, бесконечное количество корней.

Задача 3. Найти корень трансцендентного уравнения

X sin(x)+ cos(x) =25,

ближайший x=1.

Набираем задачу описанным выше способом и находим значение х.

Однако получить решение при начальном приближении 10 нам не удастся.

Маткад позволяет решать системы линейных алгебраических уравнений в матричной форме. Решение можно получить двумя способами.

1 способ.

Как известно, система линейных алгебраических уравнений в матричной форме имеет вид:

AX=B где

А – квадратная матрица коэффициентов,

X – вектор- столбец неизвестных,

В – вектор – столбец правых частей.

Решение системы в матричной форме: X= A^-1 B.

Решим в матричной форме систему

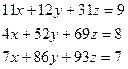
. Для этого (см. рисунок 2):

1)Наберем ORIGIN:=1. Как говорилось выше, это означает, что счет элементов будет производиться не от нуля, а с единицы.

2)Введем матрицу А.

3).Введем вектор – столбец В.

4).Набор выражения для Х желательно выполнять, используя соответствующую кнопку матричной панели.

5. После этого наберем X= и сразу получим вектор ответа.

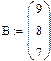
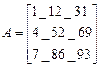
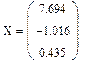
Рис.2.Решение системы линейных уравнений в матричной форме

Дата добавления: 2015-06-27