Аппроксимация сплайнами

Кусочно-линейная аппроксимация.

Аппроксимация функций.

ЛАБОРАТОРНАЯ РАБОТА №6.АППРОКСИМАЦИЯ И ОБРАБОТКА НАБЛЮДЕНИЙ В МАТКАДЕ

Пример1.

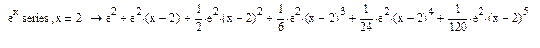
Задача 7. Разложить в ряд Тейлора около заданных значений х, с заданным числом членов функции:

А) Sin(2x) - около 1, 5 членов ряда.

Б)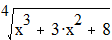

около х=3 с 5 членами разложения.

Кусочно-линейная аппроксимация производится функцией linterp(vx, vy,x)

Здесь vx- вектор аргументов x точек, через которые должна пройти кривая,

vy - вектор ординат y тех же точек, x –значение аргумента аппроксимирующей функции.

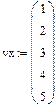
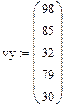
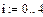
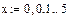
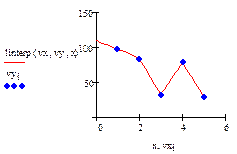
Рис.1. Кусочно-линейная аппроксимация.

Задача1. Провести кусочно-линейную аппроксимацию приведенного примера.

При небольшом числе узловых точек (менее 10) линейная интерполяция оказывается довольно грубой. При ней даже первая производная функции аппроксимации испытывает резкие скачки в узловых точках. Для целей экстраполяции функция linterp не предназначена и за пределами области определения может вести себя непредсказуемо.

Гораздо лучшие результаты дает сплайн-аппроксимация. При ней исходная функция заменяется отрезками квадратных или кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так, чтобы непрерывными были первая и вторая производные. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закрепленную в узловых точках (отсюда и название аппроксимации: splain - гибкая линейка).

Для осуществления сплайновой аппроксимации система Маткад предлагает четыре встроенные функции. Три из них служат для получения векторов вторых производных сплайн-функций при различном виде интерполяции:

cspline (VX, VY) - возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному;

pspline (VX, VY) - возвращает вектор VS вторых производных при приближении к опорным точкам параболической кривой;

lspline (VX, VY) - возвращает вектор VS вторых производных при приближении к опорным точкам прямой. Наконец, четвертая функция

interp (VS, VX, VY, x) возвращает значение у(х) для заданных векторов VS, VX, VY и заданного значения x.

Таким образом, сплайн-аппроксимация проводится в два этапа. На первом с помощью функций cspline, pspline или Ispline отыскивается вектор вторых производных функции у(х), заданной векторами VX и VY ее значений (абсцисс и ординат). Затем, на втором этапе для каждой искомой точки вычисляется значение у(х) с помощью функции interp.

На рис 2 приведен пример аппроксимации квадратическими (параболическими) сплайнами. Аппроксимация проведена для тех же заданных точек, что и в предыду­щем примере. Набраны вектора vx, vy и с помощью функции pspline получены ко­эффициенты сплайнов. Чтобы убедиться, что аппроксимирующая кривая проходит через заданные точки, функция interp вычислена для заданных значений х. По­этому результатом interp явились заданные значения у. Чтобы более точно просмотреть аппроксимирующую кривую для графика х задан в том же интервале, но с шагом 0.1. Как видим из графика, аппроксимация сплайнами совершенно не похожа на кусочно-линейную аппроксимацию.

В функции interp – vx,vy - те же векторы заданных значений, а vs – вектор

коэффи­циентов уравнений для сплайнов, полученный из функций pspline или cspline.

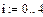
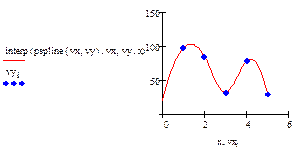
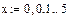
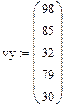
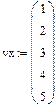
Рис.2. Аппроксимация сплайнами.

Задача 2. Набрать в Маткаде и получить графики решения для приведенного выше примера.

Дата добавления: 2015-06-27