Лабораторная работа №7. Построение законов распределения случайных величин

В Маткаде имеется целый ряд встроенных функций, позволяющих строить законы распределения случайных величин. К ним, в частности, относятся функции:

1). dnorm(x,m,s)- плотность вероятности для нормального распределения. Здесь x- случайная величина, μ- ее математическое ожидание,σ- среднеквадратическое отклонение.

2) dunif(x,a,b)- равномерная плотность вероятности, где a,b - границы интервала распре

деления. 3). dt(x,d) -плотность вероятности для распределения Стьюдента, где d- число степеней свободы. 4) dchisq(x,d) – плотность распределения χ- квадрат, где х – случайная величина, d- число степеней свободы. 5) dF(x,d1,d2) – плотность вероятности Фишера, х, d1, d2 – где – x, d1, d2, - случайная величина и две степени свободы, соответственно.

Все встроенные функции плотностей вероятностей в Маткаде начинаются с буквы d (distribution)- распределение.

Ниже приводятся примеры вычисления и построения графиков наиболее часто используемых законов распределения.

Задача 1. По заданным результатам наблюдений построить график нормального закона распределения.

Выражение для нормального закона распределения имеет вид,

где m – математическое ожидание, а σ – среднеквадратическое отклонение случайной величины х.

Поэтому, прежде всего нужно вычислить эти величины, что и показано на рис.1.

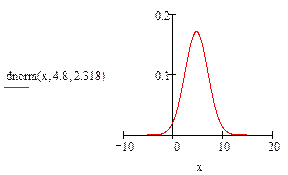
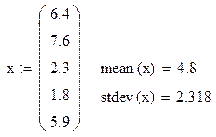
Рис.1.Построение нормального закона распределения

Задача 2. Построить равномерный закон на интервале 10-20.

Рис.2. Построение равномерного закона распределения.

Задача 3. Построить закон распределения хи – квадрат.

Распределением хи- квадрат с “d” степенями свободы называется распределение суммы квадратов “d” независимых случайных величин, каждая из которых подчинена нормальному закону распределения с математическим ожиданием, равным нулю и дисперсией, равной единице. Аналитически это распределение выражается через гамму - функцию. Закон распределения хи – квадрат используется во многих задачах математической статистики.

Рис. 3. Построение закона распределения хи – квадрат.

В Маткаде этот закон строится с помощью встроенной функции dchisq(x,d), где х – случайная величина, d- число степеней свободы:

На рис.3 показано построение закона хи – квадрат для двух значений степеней свободы

Задача 4. Построить самостоятельно закон распределения хи-квадрат с 4-мя степенями свободы для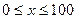

Задача 5. Построить закон z- распределения Фишера.

Распределением Фишера с “d1” и “d2” степенями свободы называется распределение F(χ), где

Здесь ξ и η - независимые, нормально распределенные случайные величины с нулевым математическим ожиданием и дисперсией, равной единице. Распределение Фишера используется в дисперсионном анализе.

В Маткаде распределение Фишера строится с помощью встроенной функции dF(x,d1,d2)., где х – случайная величина, а “d1” и “d2” – «степени свободы»

На рис.4 показано построение распределения Фишера для нескольких значений степеней свободы.

Рис. 4. Построение закона распределения Фишера.

Задача 5. Построить в Маткаде закон распределения Стьюдента.

Распределением Стьюдента или “t”- распределением называется распределение отношения

где ξ, ξ_i – независимые, нормально распределенные случайные величины с нулевым математическим ожиданием и единичной дисперсией. Параметр ‘d” называют числом степеней свободы.

Рис.5. Построение закона распределения Стьюдента.

Распределение Стьюдента широко используется в дисперсионном анализе. В Маткаде распределение Стьюдента строится встроенной функцией dt(x,d), где х – случайная величина, а “d”- число степеней свободы. На рис. 5. приведено построение этого закона для двух значений степени свободы.

Как известно, функция или интегральный закон распределения F(x) показывает вероятность попадания случайной величины х на отрезок оси абсцисс (-∞, х). и математически записывается как

где f(x) – соответствующая плотность вероятностей.

В Маткаде эти законы строятся с помощью встроенных функций

pnorm(x,m,σ)- интегральный нормальный закон распределения с математическим ожиданием m и среднеквадратичным отклонением σ;

punif(x,a,b) – интегральныйравномерный закон распределения в пределах а и b.

pchisq(x,d) – и нтегральный закон распределения хи – квадрат с “d” степенями свободы;

pF(x,d1,d2) – интегральный закон распределения Фишера со степенями свободы “d1”и”d2”.

pt(x,d) – интегральный закон распределения Стьюдента со степенью свободы “d”.

Задача 6. Построить функцию распределения для нормального закона с математическим ожиданием m=5 и среднеквадратическим отклонением σ =2.

Построение функции приведено на рис. 6.

Рис.6.Построение интегральной функции нормального закона

Задача 7. Построить функцию распределения равномерного закона в пределах а=0, b=10. Функция построена на рис. 7.

Задача 8. Построить функции распределения для распределений хи- квадрат, Фишера и Стьюдента.

Соответствующие функции построены на рис.рис. 8-10

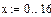
Рис.7. Построение интегрального закона Рис.8. Функция распределения хи- квадрат

равномерного распределения

.

Рис.9. Функция распределения Фишера. Рис. 10. Функция распределения Стьюдента.

Дата добавления: 2015-06-27