Решение дифференциальных уравнений с помощью функции rkfixed

Встроенная функция rkfixed (метод Рунге – Кутта с фиксированным шагом решения) позволяет решать только системы дифференциальных уравнений первого порядка.

Уравнения порядка выше первого требуется преобразовывать в систему первого порядка. Разберем сначала, как это делается применительно к пакету Маткад.

Любое обыкновенное дифференциальное уравнение выше первого порядка может быть представлено в виде системы дифференциальных уравнений первого порядка, число которых равно порядку преобразуемого уравнения. Покажем это на примере дифференциального уравнения третьего порядка.

Дано ay ''' +by '' +cy ' +dy=f(x). (1)

Введем подстановки:

y '' =y₀, (2)

y ' =y₁, (3)

y=y₂. (4)

Тогда уравнение (1) запишется в виде:

ay₀ ' +by₀+cy₁+dy₂=f(x). (5)

Это первое уравнение первого порядка будущей системы.

Продифференцируем уравнение (3). Получим

y '' =y₁ '. (4)

Левые части уравнений (2) и (4) равны. Следовательно, равны и их правые части. Отсюда

y₁ ' =y₀. (5)

Продифференцируем уравнение (4). Получим

y ' =y₂ '. (6)

Левые части уравнений (3) и (6) равны, следовательно, равны и их правые части. Тогда

y₂ ' =y_1. (7)

Мы получили систему из трех дифференциальных уравнений первого порядка:

ay₀ ' +by₀+cy₁+dy₂=f(x)

y₁ ' =y_{0 ‌‌(8)}

y₂ ' =y₁

Разрешив первое уравнение относительно производной, окончательно получим:

y₀ ' =–by₀/a–cy₁/a–dy₂/a+f(x)/a

y₁ ' =y_{0 (9)}

y₂ ' =y₁

Решим методом Рунге- Кутты с фиксированным шагом дифференциальное уравнение второго порядка:

при заданных начальных условиях t₀ =0, y(0)=1, 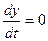и заданном конце счета t_k= 13.

Проведя преобразование в систему уравнений первого порядка, получим:

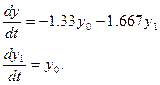
Начальные условия примут вид: y₀(0) = 0, y₁(0) = 1.

Записав правые части и начальные условия в виде векторов, получим

f(t, y) – это вектор правых частей системы. При его формировании надо обратить внимание на следующее:

1.Вместо буквы f можно использовать любую другую букву. Но тогда и во встроенной функции нужно, естественно, использовать ту же букву.

2.Внутри скобок первое имя (в нашем случае t) является именем аргумента, по которому происходит интегрирование дифференциального уравнения. Т. е. опять - таки это может быть и другая буква.

3.Вторая буква внутри скобок – это вектор имен зависимых переменных. Им эти имена полностью определяются. Если принято имя y, то именами переменных должны являться y₀, y₁, y₂ и т.д., причем первое уравнение – это

dy₀ /dt =……, второе

dy₁/dt = ……….. и т.д.

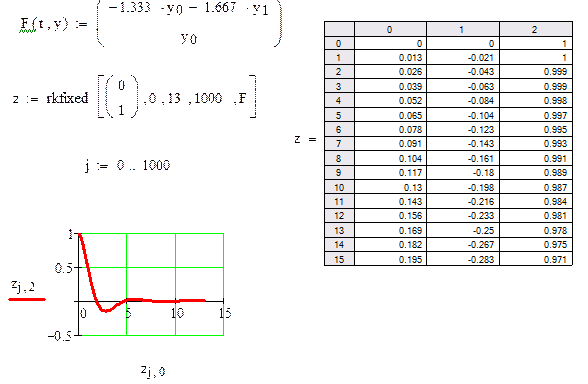
На рис. 3 приведено решение этой системы.

Р

иРис.3 Решение дифференциального уравнения с помощью функции rkfixed.

Ответ получен в виде вектора и в виде графика. В первой строке этого вектора показаны номера переменных: z₀ это время, z₁ - производная y_0, z₂ - сама функция у. Выведены только первые 11 значений вектора ответа.

Начальные условия заданы встроенным вектором v.

Ранжировка j:= 0..1000 относится не к функции rkfixed, а к графику. Для встроенной функции число точек решения задано числом 1000 внутри нее.

Внутри функции указано время интегрирования 0 –13.

По оси абсцисс графика отложен первый столбец матрицы ответов z_j,0 - аргумент (в нашей задаче – время t), где j =0..1000.

По оси ординат отложена переменная z_j,2

В процессе решения задачи на экране мигает электрическая лампочка.

Задача 1. Решить приведенную выше систему вМаткаде.

Задача 2. Решить в Маткаде дифференциальное уравнение второго порядка

T² d² y/dt² + x T dy/dt +y =0

при начальных условиях t ₀ = 0, y(t₀) =1, dy/dt (t₀) =0 и заданных значениях параметров Т=10, x =0.5.

Задача 3. Решить в Маткаде самостоятельно следующие дифференциальные уравнения:

1. 3d²y/dx² +5 dy/dx +6 y =0 x₀ =0, y(x₀) =2, dy/dx (x₀)=0.

х_лон= 20, n=500.

2. 5d³y/dt³ + 9 d²y/dt² – 2dy/dt + 8y = 1/(t+1). y(0)=0, y`(0)=1, y``(0)=0.

Задача 4. Построение фазовых портретов.

Фазовым портретом называется график функции в координатах y`(y). Фазовые портреты используются в теории автоматического управления для определения переходных процессов в автоматических системах.

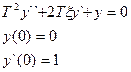Построим фазовый портрет для дифференциального уравнения второго порядка, записанного в форме:

:

Здесь Т- постоянная времени, ξ – коэффициент затухания.

Решаются три одинаковых дифференциальных уравнения с одинаковыми начальными условиями, но с разными коэффициентами затухания.

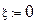
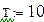
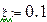
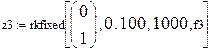
Рис.4. Фазовые портреты

Все три решения начинаются в одной точке (0,1). Но первая сплошная кривая при ξ=0 – эллипс, характеризует консервативную систему, незатухающие гармонические колебания.

Вторая пунктирная кривая при ξ=0.1 – затухающая кривая, характеризует затухающие колебания, такая система является устойчивой (это характерно для всех 0 < ξ <1).

Третья кривая пунктиром – при ξ = - 0.1 характеризует неустойчивую колебательную систему.

Дата добавления: 2015-06-27