Решение дифференциальных уравнений с помощью функции odesolve

Задача 1. Используя встроенную функцию odesolve решить в Маткаде следующее нелинейное обыкновенное дифференциальное уравнение второго порядка с нулевыми начальными условиями:

На рис. 1. показано это решение

Итак, для решения с использованием этой функции нужно:

1. Ввести директиву given

2. Набрать дифференциальное уравнение. Знак производной набирается клавишей Ё английской клавиатуры, знак «=» - с логической панели,

3. набрать начальные условия,

4. набрать функцию odesolve,

5. сформировать график,

6. Нажать клавишу F9.

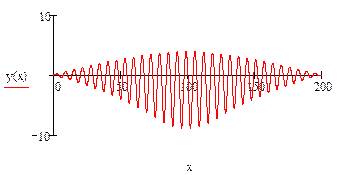
Рис.1. Решение в Маткаде обыкновенного дифференциального уравнения с помощью встроенной функции odesolve

Задача 2. Используя функцию odesolve, решить самостоятельно приведенные ниже дифференциальные уравнения. Построить графики решения:

Используя функцию odesolve, можно решать и системы дифференциальных уравнений первого порядка. На рис.2 приведено решение системы двух уравнений.

Из рисунка видно, что в функцию odesolve помимо прежних данных вводится вектор имен решаемых функций

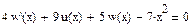
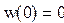
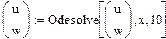
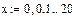
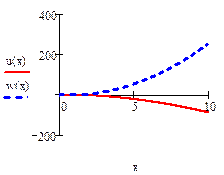
Рис.2.Решение системы уравнений первого порядка.

Недостатком этой функции является фиксированная нижняя граница аргумента

Задача 3. Решить самостоятельноприведенные ниже системы уравнений первого порядка

Дата добавления: 2015-06-27