Символьное решение линейных дифференциальных уравнений

Пример решения нелинейного уравнения

Исследование нелинейных дифференциальных уравнений.

Если решение линейных дифференциальных уравнений полностью определяется параметрами (коэффициентами) этих уравнений, то решение нелинейных уравнений зависит также и от величины возмущений.

Рассмотрим решение двух одинаковых нелинейных дифференциальных уравнений с различными начальными условиями.

d²y/dt² +1,53 dy/dt *y +0,16y=0 d²z/dt² +1,53dz/dt*z +0,16z =0

t₀ =0, y₀ =0,5, dy/dt _t=0 =0 t₀=0, z₀ =3, dz/dt _t=0 =0.

На рис.2 показаны решения обоих уравнений.

Рис.2. Влияние начальных условий на решение нелинейного дифференциального уравнения.

Вывод: При изменении начальных условий изменилась форма кривой, период колебаний.

Задача 2. Решить оба уравнения, построить графики.

Встроенных функций для символьного решения дифференциальных уравнений в Маткаде нет. Символьное решение линейных дифференциальных уравнений проводится классическим способом, через решение характеристического уравнения с последующим определением констант методом вариации постоянных.

Так как алгебраические уравнения с буквенными коэффициентами выше третьей степени не решаются в Маткаде символьно, то и линейные дифференциальные уравнения с буквенными коэффициентами выше третьего порядка решены быть не могут

Разберем символьное решение следующего линейного дифференциального уравнения третьего порядка

Его характеристическое уравнение:

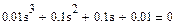
Мы решаем его символьно

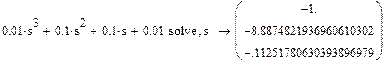
Однако полученные корни имеют слишком много знаков. Для уменьшения числа значащих цифр найдем эти корни с одновременным переводом их с помощью оператора float (плавающая точка) в форму с плавающей точкой.

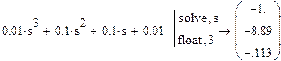
Поставив float 3, мы ограничились тремя значащими знаками. Установка двух операторов производится автоматически нажатием последовательно двух кнопок на панели символьных вычислений.

Отсюда частные решения имеют вид:

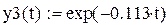
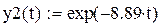
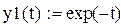
и общее решение равно

Решая систему алгебраических уравнений, определяем С1,С2,С3.

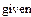
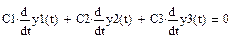
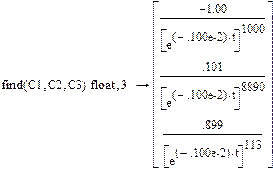
Дата добавления: 2015-06-27