Используя оператор simplify(упростить. Соответствующая кнопка символьной панели), упрощаем найденное решение

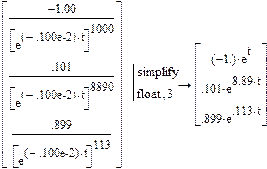
Интегрируем

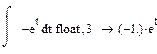
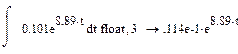
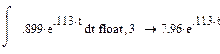
Прибавляем постоянные интегрирования

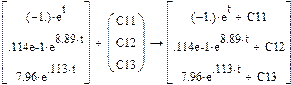
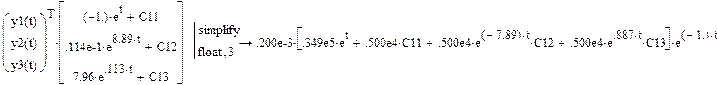Формируем общее решение

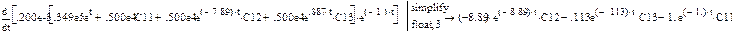Для определения констант дифференцируем два раза с упрощением

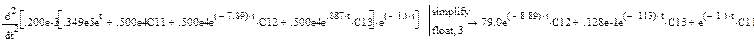
Приравнивая нулю время t, составляем уравнения для определения констант

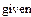
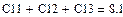
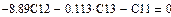
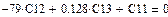
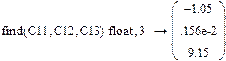
Общее решение принимает вид:

Упрощаем выражение:

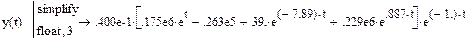
Окончательное выражение для общего решения:

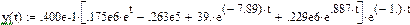
Строим график:

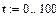
ЛАБОРАТОРНАЯ РАБОТА №3. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ.

Краевая задача решается в Маткаде методом пристрелки с помощью встроенной функции sbval. Эта функция на основании заданных конечных условий вычисляет начальные условия. После этого задача сводится к задаче Коши и ее можно решить, используя известную функцию rkfixed.

Функция sbval имеет вид sbval(v,x1,x2,f,load,score).

Здесь: v -вектор незаданных начальных условий, т.е. тех начальных условий, вместо которых заданы конечные условия. Обычно выбираем все компоненты v, равными 1;

x1, x2 - начальное и конечное значения аргумента, т.е. интервал решения дифференциального уравнения;

f(x,y)- векторная функция, содержащая правые части дифференциального уравнения, та же, что используется при решении дифференциального уравнения с помощью rkfixed;

load(x_1,v) -вектор всех начальных условий. Сюда помещаются все заданные начальные условия, а вместо незаданных помещаются компоненты вектора v;

score(x2, y)- вектор конечных условий, в который помещаются разности между текущими значениями тех переменных, для которых заданы конечные условия, и их численными значениями.

Задача 1. Задано однородное дифференциальное уравнение пятого порядка

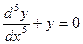
Задан интервал решения:0,1.

Для уравнения пятого порядка должны быть заданы пять граничных условий.

Заданы начальные условия y(0)=0, dy/dx _x=0 =7

и конечные условия y(1) = 1, dy/dx _x=1 = 10, d2y/dx²_x=1 = 5.

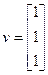Сформируем для трех не заданных начальных условий вектор v,присвоив всем его элементам единичные значения

Сформируем вектор f(x,y). Для этого введем подстановки:

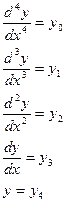
Вместо одного уравнения пятого порядка мы имеем теперь систему из пяти уравнений первого порядка:

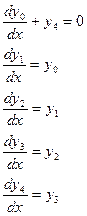
Разрешив первое уравнение этой системы относительно производной, получим:

_.

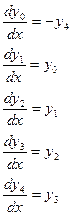
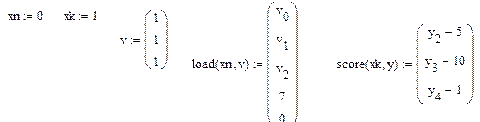
Следовательно,

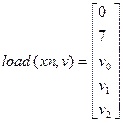
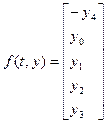
Сформируем вектор

Здесь xn - начальное значение x, а вектор заполняется следующим образом: была проведена подстановка

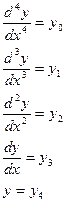
После которой вектор переменных приобрел следующий вид:

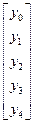
С учетом подстановки нам заданы y₀ = 0 и y₁=7. Остальные начальные условия неизвестны и мы заполняем их вектором v.

Сформируем вектор score(xk,y) для заданных конечных условий:

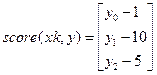
Вектор включает те переменные, для которых заданы конечные значения.

Все вышеперечисленные действия были произведены в Маткаде, и было получено искомое решение, приведенное на рис.1.

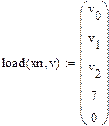
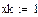
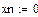
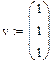
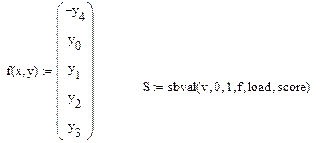
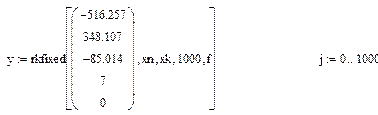
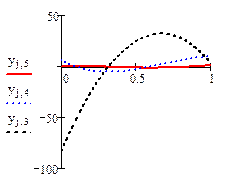
Рис.1 решение краевой задачи в Маткаде.

Функция sbval вычисляет неизвестные начальные условия, а мы затем вводим их в функцию rkfixed и получаем решение.

На графиках приведены те кривые, для которых заданы конечные условия, чтобы можно было убедиться в их выполнении, а именно y₃(x), y₄ (x), y₅(x).

Ниже приведены вычисленные начальные и конечные значения переменных. Весь диапазон решения разбит нами на 1000 точек (j=0..1000), поэтому y_0,0 - это начальное, а y_1000,0 - конечное значения y₀. То же относится к другим переменным.

Как видим, вычисленные значения совпадают с заданными.

Задача 1. Решить приведенное уравнение в Маткаде.

Задача 2. Задано линейное дифференциальное уравнение с переменными коэффициентами (другое название - нестационарное): .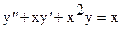

В таких уравнениях коэффициенты при переменной являются функцией независимой переменной - аргумента, в нашем случае х.

Задан интервал вычислений 0<= x <=5, заданы конечные условия y(5) =2, .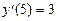

Нестационарные дифференциальные уравнения относятся к классу линейных, однако их аналитическое решение обычно затруднено, и их проще решать численно.

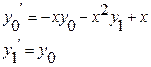Перейдя к системе дифференциальных уравнений первого порядка, имеем (проделать самостоятельно):

Далее составляем все необходимые функции, как показано на рисунке и проводим решение.

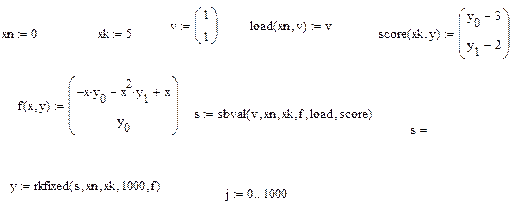
Рис.2. Решение краевой задачи для нестационарного дифференциального уравнения

Это уравнение является сложным для компьютера, что видно из длительности его решения.

Проверим вычисление крайних точек:

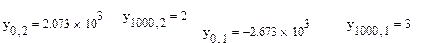
Как видим, конечные значения совпали с заданными.

Дата добавления: 2015-06-27