Дифференциальныеt уравнения со случайной составляющей

Решение дифференциальных уравнений методом Буль-Штейера

Электронный учебник по Маткаду утверждает, что численный метод Буль – Штейера дает более точное решение, чем метод Рунге Кутта. Ниже на рис.5 приведено решение этим методом нелинейной системы второго порядка:

с начальными условиями

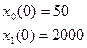
Из рисунка видно, что последовательность решения не отличается от последовательности решения методом Рунге-Кутта.

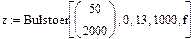
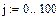
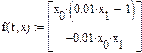
Рис.5.Решение дифференциального уравнения методом Буль - Штейера

Маткад позволяет решать дифференциальные уравнения, коэффициенты которого являются случайными функциями. При этом, конечно, каждая реализация решения будет отличаться от предыдущей. Ниже, на рис.6 показано решение уравнения третьего порядка, свободный член которого реализуется функцией rnd –возвращающей равномерно распределенную случайную величину в пределах 0 – 1.

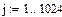
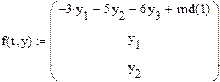
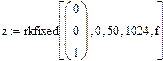
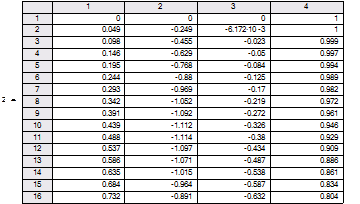
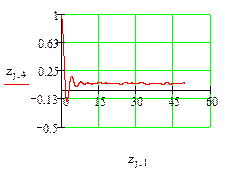
Рис.6 Решение дифференциального уравнения со случайными параметрами

ЛАБОРАТОРНАЯ РАБОТА №2.РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В МАТКАДЕ (ЗАДАЧА КОШИ)

Дата добавления: 2015-06-27