Из графика ясно видно, что между группами людей разного возраста есть разница в уровне дохода. Чем выше возраст, тем больше доход

Аналогичные операции проведём для взаимодействия нескольких факторов. В диалоговом окне Таблица всех эффектов выберем Пол * Возраст и нажмём ОК.

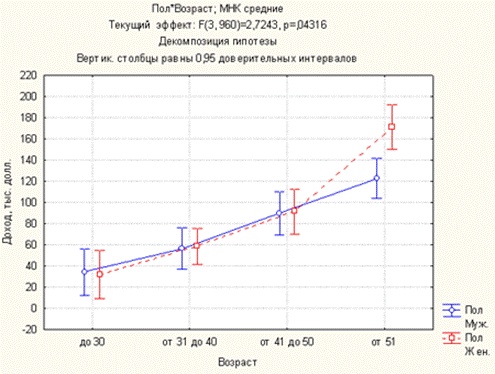
Рис. 11. График зависимости среднего дохода от пола и возраста

Получен неожиданный результат: для опрошенных людей в возрасте до 50 лет уровень дохода растёт с возрастом и не зависит от пола; для опрошенных людей старше 50 лет женщины имеют значимо больший доход, чем мужчины. Стоит построить полученный график в разрезе уровня образования. Возможно, такая закомерность нарушается в некоторых категориях или, наоборот, носит универсальный характер. Для этого выберем Уровень образования * Пол * Возраст и нажмём ОК.

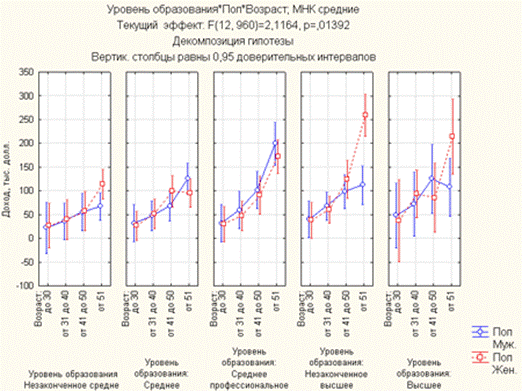
Рис. 12. График зависимости среднего дохода от пола, возраста, уровня образования

Видим, что полученная зависимость не характерна для среднего и среднего профессионального образования. В остальных случаях она справедлива.

6 шаг. Анализ результатов – оценка качества модели. Выше в основном использовались графические средства дисперсионного анализа. Рассмотрим некоторые другие полезные результаты, которые можно получить. Во-первых, интересно посмотреть, какую долю изменчивости объясняют рассматриваемые факторы и их взаимодействия. Для этого во вкладке Итоги нажмём на кнопку Общая R модели. Появится следующая таблица.

Рис. 13. Таблица SS модели и SS остатков

Число в столбце Множеств. R2 – квадрат множественного коэффициента корреляции; оно показывает, какую долю изменчивости объясняет построенная модель. В нашем случае R2 = 0.195, что говорит о невысоком качестве модели. В самом деле, на уровень дохода влияют не только факторы, внесённые в модель.

7 шаг. Анализ результатов – анализ контрастов. Часто требуется не только установить различие в среднем значении зависимой переменной для разных категорий, но и установить величину различия для заданных категорий. Для этого следует исследовать контрасты. Выше было показано, что уровень дохода для мужчин и женщин значимо отличается для возраста от 51, в остальных случаях различие не значимо. Выведем разницу в уровне дохода для мужчин и женщин в возрасте выше 51 года и между 40 и 50 годами. Для этого перейдём во вкладку Контрасты и выставим все значения следующим образом.

Рис. 14. Вкладка Контрасты

При нажатии кнопки Вычислить появится несколько таблиц. Нас интересует таблица с оценками контрастов.

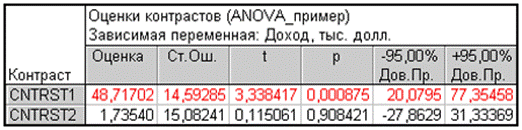
Рис. 15. Таблица Оценки контрастов

Можно сделать следующие выводы: для мужчин и женщин старше 51 года разница в уровне дохода составляет 48,7 тыс. долл. Разница значима; для мужчин и женщин в возрасте от 41 до 50 лет разница в уровне дохода составляет 1,73 тыс. долл. Разница не значима. Аналогично можно задать более сложные контрасты или воспользоваться одним из заранее заданных наборов.

8 шаг. Дополнительные результаты. Используя остальные вкладки окна результатов можно получить следующие результаты: средние значения зависимой переменной для выбранного эффекта – вкладка Средние; проверка апостериорных критериев (post hoc) – вкладка Апостериорные; проверка сделанных для проведения дисперсионного анализа предположений – вкладка Предположения; построение профилей отклика/желательности – вкладка Профили; анализ остатков – вкладка Остатки; вывод матриц, используемых в анализе – вкладка Матрицы; доступ к опциям отправки спецификаций переменных, кода анализа и предсказанного уравнения в отчёт, а также создании кода модели на языках C/C++/SVB/PMML – вкладка Отчёт. Результаты доступны как в численном, так и в графическом видах.

Пример 1. Тест точности вычислений при малой относительной дисперсии. В приведённом ниже тестовом наборе данных переменная var2 (второй столбец), имеющая небольшую относительную дисперсию, линейно зависит от переменной var3 (третий столбец); следовательно, коэффициент корреляции между любой переменной (напр., var1) и переменной var2 должен быть примерно равен коэффициенту корреляции между этой переменной и переменной var3.

var1	var2	var3
1.0	100000.00000001	1.0
2.0	100000.00000002	2.0
3.0	100000.00000001	1.0
4.0	100000.00000002	2.0
5.0	100000.00000001	1.0
6.0	100000.00000002	2.0
7.0	100000.00000005	5.0

Приведём два коэффициента корреляции (между переменными var1*var2 и var1*var3), вычисленных в STATISTICA при использовании алгоритма оптимизации вычислений повышенной точности и отображаемых с наибольшей доступной точностью.

variables	Pearson r	p-level
var1 * var2	0.65465367070798	0.111
var1 * var3	0.65465367070798	0.111

Пример 2. Многофакторный несбалансированный план дисперсионного анализа среднего размера. Рассмотрим план 5 х 5 х 5 х 3 (между группами) х 3 х 3 х 3 (повторные измерения) с неодинаковым числом наблюдений в группах. То есть, имеем 375 групп и 27 зависимых переменных (файл данных ANOVA4 может быть получен от StatSoft). Матрица межгруппового плана при наибольшем порядке взаимодействия имеет 128 степеней свободы. Ниже приведены результаты одномерного и многомерного дисперсионного анализа при взаимодействии наивысшего порядка.

css/3: general manova	INTERACTION: 1 х 2 х 3 х 4 х 5 х 6 х 7 1 – IV1, 2 – IV2, 3 – IV3, 4 – IV4, 5 – RFACT1, 6 – RFACT2, 7 – RFACT3
Univar. Test	Sum of Squares	df	Mean Square	F	p-level
Effect Error	8664.99 24854.14		8.461903 8.262680	1.02411	.31744

css/3: general manova	INTERACTION: 1 х 2 х 3 х 4 х 5 х 6 х 7 1 – IV1, 2 – IV2, 3 – IV3, 4 – IV4, 5 – RFACT1, 6 – RFACT2, 7 – RFACT3
Test	Value	p-level
Wilk’s Lambda Rao R (1024, 2966) Pillai-Bartlett Trace V (1024, 3008)	.088651 1.027036 2.071145 1.026166	.29812 .30355

Дата добавления: 2015-06-28