Основные показатели динамики экономических явлений

Показатели динамики могут быть рассчитаны либо базисным, либо цепным способом. В основе расчета лежит сравнение уровней временного ряда. Если сравнение осуществляется с одним и тем же показателем, принятым за базу сравнения (y_б), то показатели называются базисными (во временных рядах часто за базу сравнения берется первый уровень ряда y₁). Если каждый уровень (y_t) сравнивается с предыдущим (y_{t- 1}), то вычисленные показатели называются цепными.

Показатель динамики	Способ расчета
базисный	цепной
Абсолютный прирост
Темп роста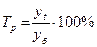
Темп прироста

Абсолютный прирост определяется как разность двух сравниваемых уровней и показывает скорость изменения уровней ряда. Если цепные абсолютные приросты со временем возрастают, то исследуемое явление развивается с ускорением. Ускорение абсолютного прироста – это разность между абсолютными приростами, вычисленными цепным способом. Абсолютное ускорение позволяет увидеть, насколько данная скорость (абсолютный прирост) больше или меньше предыдущей.

Темп роста характеризует отношение двух сравниваемых уровней ряда, выраженное в процентах. Показатели, выраженные в коэффициентах, принято называть коэффициентами роста. Цепные темпы роста характеризуют интенсивность изменения уровней от года к году, базисные – фиксируют интенсивность роста (снижения) за весь интервал времени между текущими и базисными уровнями.

Темп прироста характеризует абсолютный прирост в относительных величинах. Определенный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения.

Если систематически растут цепные темпы роста или прироста, то ряд развивается с относительным ускорением, которое можно определить как разность следующих друг за другом темпов роста или прироста. Полученная величина выражается в процентных пунктах (п.п.).

Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за этот же промежуток времени или как сотую часть уровня предыдущего периода.

Для получения обобщающих показателей динамики развития определяются средние величины: средний абсолютный прирост, средние темпы роста и прироста. Величина среднего абсолютного прироста показывает скорость развития явления за изучаемый интервал времени и вычисляется по формуле:

где n - длина временного ряда.

Для определения средней скорости изменения явления за рассматриваемый период времени вычисляют средний темп роста. Этот показатель рассчитывают по формуле средней геометрической:

Средний темп прироста соответственно равен:

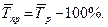
Средний уровень интервального ряда с равностоящими уровнями определяется по формуле средней арифметической:

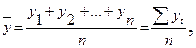
Средний уровень моментного ряда с равностоящими уровнями определяется по формуле средней хронологической:

Если определяются средние уровни для рядов с неравностоящими уровнями, то используются формулы взвешенных средних величин.

Дата добавления: 2015-06-28