Простейшие методы прогнозирования рядов динамики

Один из наиболее распространенных и простых методов прогнозирования заключается в экстраполяции, т.е. в продлении в будущее тенденции, наблюдавшейся в прошлом. Основная цель данного прогноза заключается в том, чтобы показать, к каким результатам можно прийти в будущем, если развитие явления будет происходить со скоростью, ускорением и так далее, аналогичным прошлого периода.

Широкое практическое применение методов экстраполяции объясняется простотой метода, сравнительно небольшим объемом информации и четкостью механизма реализации, лежащих в его основе предпосылок. Теоретической основой распространения тенденции на будущее является свойство социально-экономических явлений, называемое инерционностью, которое проявляется в сохранении во времени тенденций, закономерностей, взаимосвязей с другими явлениями.

В зависимости от того, какие исходные данные положены в основу прогноза, выделяют следующие простейшие методы экстраполяции (прогнозирования):

1. Экстраполяция на основе среднего уровня применяется при предположении о том, что средней уровень не имеет тенденции к изменению или это изменение незначительно. В этом случае прогнозируемый уровень равен среднему значению уровней в прошлом, т.е.

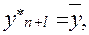
где прогнозируемое значение уровня в точке n+l;

l - период упреждения (прогноза);

- средний уровень ряда Y_t. (где средний уровень ряда определяется по средней арифметической по формуле .)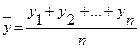

2. Экстраполяция на основе среднего абсолютного прироста может быть выполнена в том случае, если есть уверенность в равномерном изменении уровней (на равномерный характер развития указывают примерно одинаковые значения цепных абсолютных приростов).

В этом случае прогнозирование осуществляется по следующей формуле:

где

y_n - фактическое значение в последней n- ой точке ряда,

l - период упреждения,

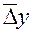- значение среднего абсолютного прироста его значение может быть определено по формуле .

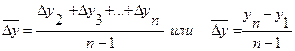3. Экстраполяция на основе среднего темпа (коэффициента) роста применяется для прогнозирования процессов, описание динамики которых соответствует представлению в виде показательной (экспоненциальной) кривой (на это указывают примерно одинаковые значения цепных темпов роста или прироста). В этом случае прогнозное значение на l шагов вперед определяется по следующей формуле:

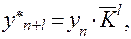
где 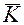- средний коэффициент роста, рассчитанный для ряда Y_t, который определяется как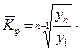

Рассмотренные методы прогнозирования являются простейшими, и поэтому прогнозы, полученные на их основе, являются приближенными и при увеличении периода упреждения не всегда надежны. Как правило, эти методы используются только при краткосрочном прогнозировании и при предположении, что в будущем тенденция развития явления не изменится.

Если кривые роста используются для прогнозирования, то их применение должно базироваться на предположении о неизменности, сохранении основной тенденции, как на всем периоде наблюдений, так и в прогнозируемом периоде. Если есть основания принять эти допущения, то прогнозные значения можно найти путем подстановки в уравнение кривой значений времени t, соответствующих периоду упреждения (т.е. t = n+ 1, …, n+l). Полученный таким образом прогноз называют точечным. Но, как правило, при прогнозировании социально - экономических показателей «фактическое попадание в точку» маловероятно, и поэтому, прогноз должен быть определен в виде интервала значений.

Несовпадение фактических данных с точечным прогнозом, полученным путем экстраполяции, может быть вызвано: 1) ошибочностью выбора формы линии тренда; 2) погрешностью оценивания параметров кривой роста; 3) погрешностью, связанной с отклонениями отдельных наблюдений от тренда.

В общем виде доверительный интервал прогноза определяется как

- точечный прогноз на период t = n + l;

t_a - значение t -статистики Стьюдента,

S_y - среднее квадратическое отклонение фактических данных от расчетных, 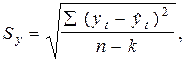а k - число оцениваемых параметров выравнивающей кривой.

74. Индексы сезонности.

Индексы сезонности используются в анализе сезонных колебаний, которые проявляются периодически, регулярно повторяются из месяца в месяц, или из квартала в квартал каждый год.

Эти колебания является результатом природных, общественных и социально-экономических факторов. Сезонные колебания проявляются с различной степенью интенсивности в различных сферах жизни общества: неодинаковое потребление электроэнергии в течение года; ярко-выраженный сезонный характер имеет сельское хозяйство, что вызывает неравномерность работы перерабатывающих предприятий, а это в свою очередь вызывает сезонные колебания в торговле. Сезонность также возникает из-за сезонного спроса на товары народного потребления (обувь, одежда) и т.д. Но, как бы, ни проявлялась сезонность, она всегда наносит ущерб деятельности фирм, который проявляется в неравномерном использовании оборудования и рабочей силы, неравномерной поставке сырья, загрузке транспорта и т.д.

При изучении сезонных колебаний и расчете индексов сезонности необходимо иметь данные по кварталам или месяцам не менее чем за три года. Индексы сезонности показывают, на сколько процентов в среднем отличается значение показателя в определенном квартале (месяце) относительно среднегодового уровня..

Для вычисления индексов необходимо учитывать наличие основной тенденции во временном ряду.

1. Если временной ряд не содержит ярко-выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по фактическим данным без предварительного выравнивания.

Для каждого месяца (квартала) рассчитывается средняя величина уровня 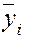, затем вычисляется средний уровень для всего ряда 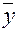и определяется процентное соотношение средних для каждого месяца к общему среднему уровню ряда, т.е. индексы сезонности определяются как

где i = 1, 2,..., 12, если данные помесячные, или i = 1, 2, 3, 4, если данные поквартальные.

2. Если временной ряд содержит определенную тенденцию в развитии, то прежде, чем вычислить индексы сезонности, по фактическим уровням выявляется основная тенденция, которая может быть выражена с помощью аналитического выравнивания, т.е. определяется уравнение тренда;

Далее по уравнению тренда для всех t = 1, 2, …, n вычисляются расчетные значения и определяются показатели сезонности, как процентное отношение фактических уровней y_t к соответствующим расчетным уровням 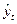(для всех t = 1, n)

Индексы сезонности находятся как средние арифметические из показателей сезонностипо одноименным периодам (либо по месяцам, либо по кварталам).

Расчет индексов заканчивается проверкой, которая заключается в определении среднего индекса сезонности 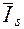. Этот индекс должен быть равен 100%.

Дата добавления: 2015-06-28