Проекции пирамиды

Построение проекций трехгранной пирамиды на­чинается с построения основания, горизонтальная проекция которого представляет собой действи­тельный вид треугольника (рис.9, а). Фронталь­ная проекция основания изображается горизонталь­ным отрезком прямой.

Из горизонтальной проекции s вершины пира­миды проводят вертикальную линию связи, на ко­торой от оси х откладывают высоту пирамиды и получают фронтальную проекцию s' вершины. Соединяя точку s' с точками 1', 2' и 3', получают фронтальные проекции ребер пирамиды.

Горизонтальные проекции ребер получают соеди­няя горизонтальную проекцию s вершины пира­миды с горизонтальными проекциями 1, 2 и 3 вер­шин основания.

Пусть, например, дана фронтальная проекция а' точки А, расположенной на грани 1s2 пирамиды, и требуется найти другую проекцию этой точки. Для решения этой задачи проведем через а' вспомо­гательную прямую и продолжим ее до пересечения с фронтальными проекциями l's' и 2's' ребер в точ­ках n' и m'. Затем проведем из точек n' и m' линии связи до пересечения с горизонтальными проекция­ми 1s и 2s этих ребер в точках n и m. Соединив n с m, получим горизонтальную проекцию вспомога­тельной прямой, на которой с помощью линии свя­зи найдем искомую горизонтальную проекцию α точки А. (Профильную проекцию этой точки на­ходят обычным приемом, используя линии связи).

Рис. 9 – Проекции пирамиды

Второй способ решения задачи на построение проекции точки по одной заданной, показан на рис.9, б для четырехгранной правильной пира­миды. В этом случае через заданную фронтальную проекцию а' точки А проводят вспомогательную прямую, проходящую через вершину пирамиды и расположенную на ее грани. Горизонтальную проекцию ns вспомогательной прямой находят при­меняя линию связи. Искомая горизонтальная про­екция а точки А находится на пересечении линии связи, проведенной из точки а' с горизонтальной проекцией ns вспомогательной прямой.

Фронтальная диметрическая проекция правиль­ной четырехгранной пирамиды выполняется сле­дующим образом (рис.9, в).

Вначале строят основание, для чего по оси х' от­кладывают длину диагонали 1131, а по оси y' - по­ловину длины диагонали 2141 (или 11З1). Из точки о пересечения диагоналей проводят прямую, парал­лельную оси o'z', и на этой прямой откладывают высоту пирамиды. Вершину S' соединяют с верши­нами основания прямыми линиями–ребрами.

Фронтальную диметрическую проекцию точки А, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного черте­жа. От начала координат о' по оси о'х' отклады­вают координату хА, из ее конца параллельно оси о'у' - половину координаты уА и из конца этой координаты параллельно оси o'z'- третью коорди­нату zA. Построение диметрии точки В более про­стое. От точки о' по оси о'х' откладывают коорди­нату хв и из конца ее проводят прямую, парал­лельную оси o'z', до пересечения с ребром пира­миды в точке В'.

Проекции цилиндра

Боковая поверхность прямого кругового цилин­дра образована движением отрезка А В вокруг вер­тикальной оси по направляющей окружности. На рис.10, а дано наглядное изображение цилиндра.

Построение горизонтальной и фронтальной про­екций цилиндра показано на рис.10,б и в.

Построение начинают с изображения основа­ния цилиндра, т.е. двух проекций окружности (рис.10,б). Так как окружность расположена на плоскости Н, то она проецируется на эту плоскость без искажения. Фронтальная проекция окружности представляет собой отрезок горизонтальной пря­мой линии, равный диаметру окружности основа­ния.

Рис. 10 – Проекции цилиндра

После построения основания на фронтальной проекции проводят две очерковые (крайние) обра­зующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, который является фронтальной проекцией верхнего основания цилиндра (рис.10, в).

Определение двух недостающих проекций точек А и В, расположенных на поверхности цилиндра, по одной заданной, например, фронтальной проекции в данном случае затруднений не вызывает, так как вся горизонтальная проекция боковой поверхности цилиндра представляет собой окружность (рис.11). Следовательно, горизонтальные проек­ции точек А и В можно найти, проводя из данных точек а' и b' вертикальные линии связи до их пере­сечения с окружностью в искомых точках а и b.

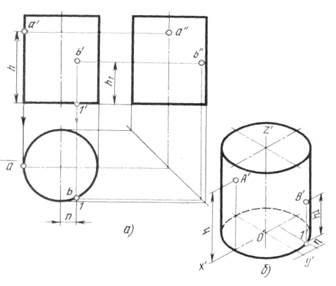
Рис. 11 – Проекции точек на цилиндре

Профильные проекции точек А и В строят также при помощи вертикальных и горизонтальных ли­ний связи.

Изометрическую проекцию цилиндра вычерчи­вают, как показано на рис.11,б.

Изометрию точек А и В строят по их координа­там. Например, для построения точки В от начала координат о' по оси о'х' откладывают координату хв = n, а затем через ее конец проводят прямую, параллельную оси о'у', до пересечения с эллипсом или овалом (основанием) в точке1'. Из этой точки параллельно оси o'z' проводят прямую, на которой откладывают координату z_B= h₁ точки В.

Проекции конуса

Наглядное изображение прямого кругового кону­са показано на рис.12, а. Боковая поверхность ко­нуса образована вращением образующей BS около оси конуса по направляющей - окружности основа­ния. Последовательность построения двух проекций конуса показана на рис.12, б и в. Предварительно строят две проекции основания. Горизонтальная проекция основания - окружность. Если предполо­жить, что основание конуса лежит на плоскости Н, то фронтальной проекцией будет отрезок прямой, равный диаметру этой окружности (рис.12, б). На фронтальной проекции из середины основания во­сставляют перпендикуляр и на нем откладывают высоту конуса (рис.12, в). Полученную фронталь­ную проекцию вершины конуса соединяют прямы­ми с концами фронтальной проекции основания и получают фронтальную проекцию конуса.

Рис. 12 – Проекции конуса

Если на поверхности конуса задана одна проек­ция точки А, то две другие проекции этой точки определяют с помощью вспомогательных линий — образующей, расположенной на поверхности кону­са и проведенной через точку А или окружности, расположенной в плоскости, параллельной основа­нию конуса.

В первом случае (рис.13, а) проводят фронталь­ную проекцию s'a'f' вспомогательной образующей. Пользуясь вертикальной линией связи, проведенной из точки f', расположенной на фронтальной проек­ции окружности основания, находят горизонталь­ную проекцию saf этой образующей, на которой при помощи линии связи, проходящей через а', находят искомую точку а.

Во втором случае (рис.13, б) вспомогательной линией, проходящей через точку А, будет окруж­ность, расположенная на конической поверхности и параллельная плоскости Н. Фронтальная проек­ция этой окружности изображается в виде отрезка горизонтальной прямой. Искомая горизонтальная проекция а точки А находится на пересечении ли­нии связи, опущенной из точки а' с горизонтальной проекцией вспомогательной окружности.

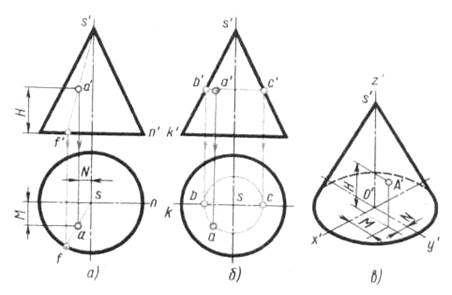
Рис. 13 – Проекции точек на конусе

Если заданная фронтальная проекция b' точки В расположена на контурной (очерковой) образую­щей SK, то горизонтальная проекция точки нахо­дится без вспомогательных линий.

Изометрическую проекцию точки А, находящейся на поверхности конуса, строят по трем координа­там точки (рис.13, в): хА = N, уА = М и zА = Н. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от начала координат о' по оси о'х' отложена координата хА = N; из конца ее параллельно оси о'у' проведена прямая, на которой отложена координата уА = М; из конца отрезка, равного М, параллельно оси o'z' проведена прямая, на которой отложена координа­та zA = Н. В результате построений получим иско­мую изометрическую проекцию точки А.

Варианты задания к листу 1-2

Построить в трех проекциях геометрические тела. Найти проекции точек, расположенных на их поверхностях. Параметры для построения брать из таблицы в соответствии со своим вариантом.

Задания 10, 15, 20, 25, 30, 35

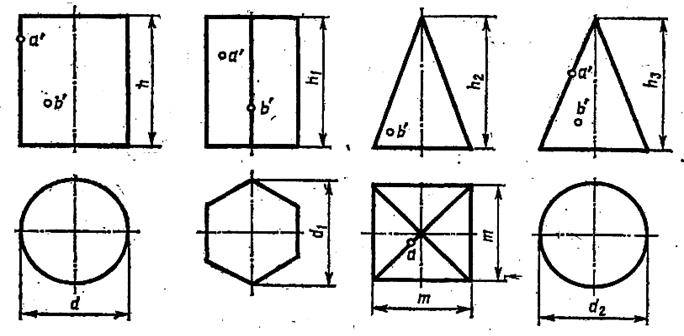
№ задания
d
d1
d2
m
h
h1
h2
h3

Задания 11, 16, 21, 26, 31, 36

Построить в трех проекциях геометрические тела. Найти проекции точек, расположенных на их поверхностях.

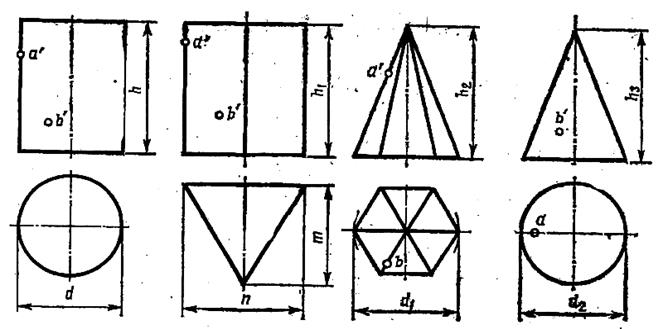
№ задания
d
d1
d2
m
п
h
h1
h2
h3

Задания 12, 17, 22, 27, 32, 37

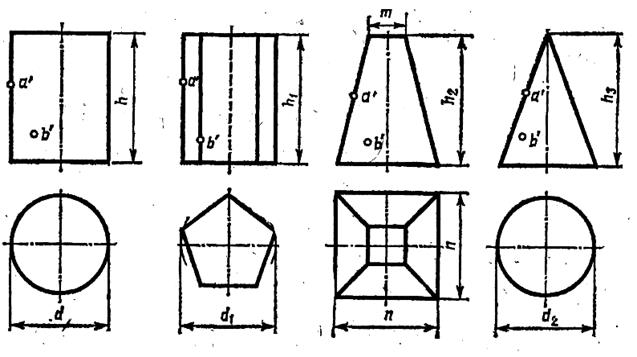Построить в трех проекциях геометрические тела. Найти проекции точек, расположенных на их поверхностях.

№ задания
d
d1
d2
п
h
h1
h2
h3

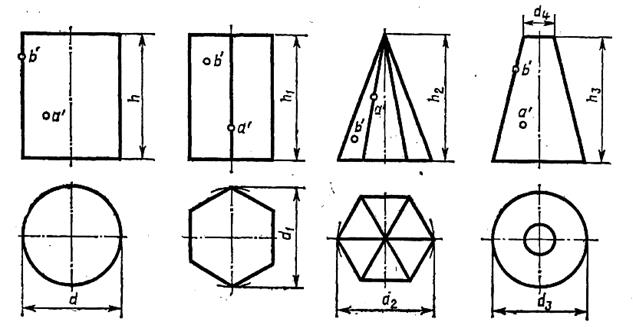
Задания 13, 18, 23, 28, 33, 38

Построить в трех проекциях геометрические тела. Найти проекции точек, расположенных на их поверхностях.

№ задания
d
d1
d2
d 3
h
h1
h2
h3

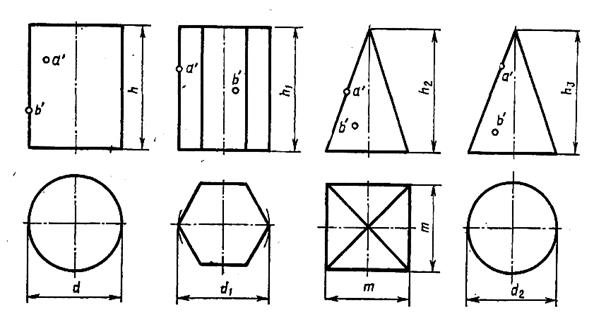
Задания 14, 19, 24, 29, 34, 39

Построить в трех проекциях геометрические тела. Найти проекции точек, расположенных на их поверхностях.

№ задания
d
d1
d2
m
h
h1
h2
h3

Дата добавления: 2015-06-28