ЛИСТ 5. Пересечение поверхностей

Целевое назначение листа: Изучить способ вспомогательных секущих плоскостей при определении линии пересечения геометрических тел.

Методические указания к листу. Как правило, детали представляют собой комбинации пересекающихся геометрических элементов, ограниченных плоскостями и кривыми поверхностями. Геометрические тела могут быть сплошными и полыми, с отверстиями, выемками и т. д. При разработке чертежа линии пересечения поверхностей должны быть построены. Перед построением линии пересечения необходимо определить: а) какие две поверхности пересекаются; б) на каких изображениях следует производить построение; в) характерные точки; г) каким методом проще ее строить.

Следует помнить, что при пересечении двух плоскостей в пересечении получается прямая линия, двух многогранников – ломаная, двух тел вращения – кривая(исключение составляют два тела вращения с одинаковым диаметром и взаимно пересекающимися осевыми линиями), тела вращения с многогранником –кривая и прямая

Каждая точка линии пересечения принадлежит одновременно поверхности одного и другого тела. При построении точек линии пересечения поверхностей вначале находят характерныеилиопорные. Остальные промежуточныеточки находят с помощью вспомогательных построений.

Метод вспомогательных секущих плоскостей заключается в том, что обе пересекающиеся поверхности мысленно рассекаются вспомогательной плоскости.

В условиях задачи фронтальная и горизонтальная проекции цилиндра даны законченными. Грани отверстия образованы фронтально проецирующими плоскостями и пересекаются между собой по отрезкам прямых, перпендикулярных к плоскости V. Их фронтальные проекции – точки, а горизонтальные проекции – отрезки прямых линий, параллельных плоскости Н. Поверхность цилиндра проецирующая. Горизонтальная проекция линии пересечения поверхностей цилиндра и отверстия принадлежит вырожденной проекции поверхности цилиндра.

Порядок выполнения листа. На листе чертежной бумаги формата А3 по фронтальной и горизонтальной проекциям, заданным в таблице 9, вычертить три проекции цилиндра, имеющего сквозное призматическое отверстие. Построить профильную проекцию линии пересечения поверхности цилиндра и отверстия, нанести размеры. Образец выполнения на рисунке 19. Изображения строить в масштабе 1:1.

Отмечаем фронтальные и горизонтальные проекции характерных точек 1, 2, 5, затем при помощи вспомогательных секущих плоскостей определяем точки 3, 4, принадлежащие линии взаимного пересечения поверхностей цилиндра и призмы, и строим профильную проекцию линии пересечения, учитывая условие видимости точек. На рисунке 18 пример пересечения цилиндра секущими плоскостями P(прямоугольник), N(окружность),F(эллипс).

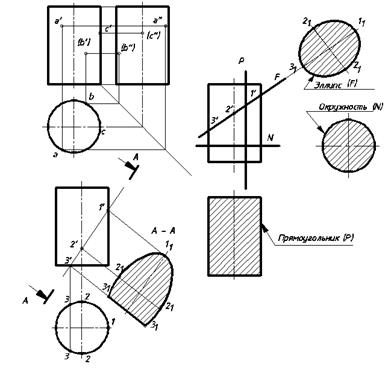
Рисунок 18 – Определение фигуры сечения цилиндра

Таблица 9 – Задания к листу 5

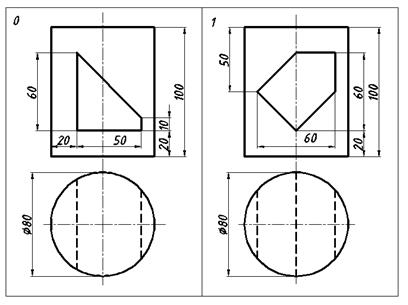
Продолжение таблицы 9

Продолжение таблицы 9

Рисунок 19 – Пример оформление листа 5

Дата добавления: 2015-06-28