Проверка гипотезы о законе нормального распределения по критерию Пирсона с помощью табличного процессора Excel

Вместо заполнения большого количества таблиц можно воспользоваться статистическими функциями.

Проверку гипотезы о законе нормального распределения выполним на примере интервального вариационного ряда, построенного в пункте 1.4.2, и статистических характеристик ряда из пункта 1.4.4.

1. Находим нормализованные значения признака (рис 1.3.). Вызываем список функций, выбираем функцию «НОРМАЛИЗАЦИЯ» (STANDATRDIZE). В поле «Х» вводим название ячейки первого интервала, во втором поле среднее значение по выборке, в третьем поле стандартное отклонение выборки. Копируем данную формулу для остальных строк.

2. По таблице плотности распределения φ(u) находим вероятность распределения этих значений и заполняем следующий столбец.

3. Следующий столбец заполняем рассчитанным выражением .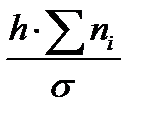

4. Находим теоретические частоты по формуле (2) и заполняем последний 8 столбец.

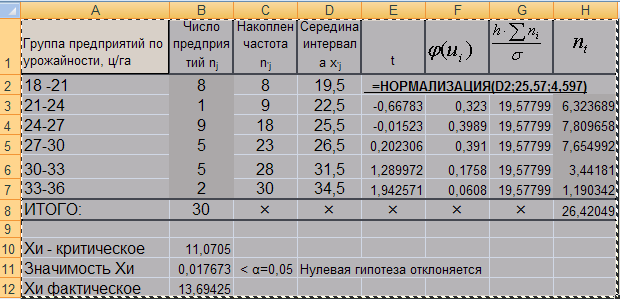
Рис. 1.3. Хи тест

5. Далее, для вычисления критерия Пирсона, воспользуемся функцией «ХИ2ТЕСТ». В поле «Фактический интервал» выделяем массив фактических частот, в поле «Ожидаемый интервал» вводим массив теоретических частот. В результате получаем значимость фактического критерия Пирсона. Чтобы получить фактическое значение критерия Пирсона, воспользуемся функцией «ХИ2ОБР». В поле «вероятность» вводим полученную значимость критерия (ячейка B11), а в поле «степени_свободы» соответствующее число степеней свободы для данной группировки. В данном случае n-1=5 (n – число групп).

Полученную в пункте 5 фактическую значимость критерия Пирсона «p» сравниваем с установленным уровнем значимости «α». Если α_факт <α= 0,05, то утверждаем, что эмпирическое распределение сходно с теоретическим и нулевая гипотеза отвергается. Далее, если нужно, мы находим фактическое значение критерия по значимости «α » и числа степеней свободы.

Дата добавления: 2015-06-28