Оценка значимости уравнения регрессии и параметров тесноты связи 1 страница

Для оценки существенности, значимости коэффициента корреляции используется t-критерий Стьюдента.

Находится средняя ошибка коэффициента корреляции по формуле:

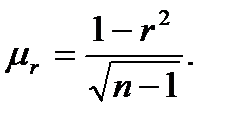
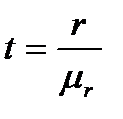
На основе ошибки рассчитывается t-критерий:

Рассчитанное значение t-критерия сравнивают с табличным, найденным в таблице распределения Стьюдента при уровне значимости 0,05 или 0,01 и числе степеней свободы n-1. Если расчетное значение t-критерия больше табличного, то коэффициент корреляции признается значимым.

При криволинейной связи для оценки значимости корреляционного отношения и уравнения регрессии применяется F-критерий. Он вычисляется по формуле:

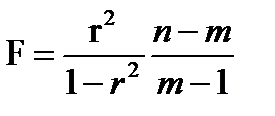
или

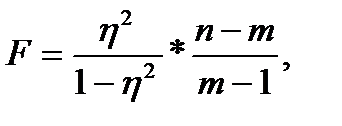
где η – корреляционное отношение; n – число наблюдений; m – число параметров в уравнении регрессии.

Рассчитанное значение F сравнивается с табличным для принятого уровня значимости α (0,05 или 0,01) и чисел степеней свободы к₁=m-1 и k₂=n-m. Если расчетное значение F превышает табличное, связь признается существенной.

Значимость коэффициента регрессии устанавливается с помощью t -критерия Стьюдента, который вычисляется по формуле:

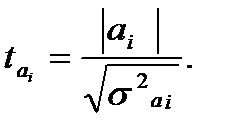
где σ²_аi - дисперсия коэффициента регрессии.

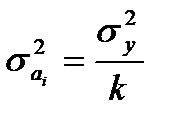
Она вычисляется по формуле:

где к – число факторных признаков в уравнении регрессии.

Коэффициент регрессии признается значимым, если t_a1≥t_кр. t_кр отыскивается в таблице критических точек распределения Стьюдента при принятом уровне значимости и числе степеней свободы k=n-1.

В данной таблице «Множественный R» - это коэффициент корреляции, «R-квадрат» - коэффициент детерминации. «Коэффициенты: Y-пересечение» - свободный член уравнения регрессии 30,30585; «Переменная Х1» – коэффициент регрессии -0,22754. Здесь имеются также значения F-критерия Фишера 0,006743, t-критерия Стьюдента 22,07752, «Стандартная ошибка 2,744412», которые необходимы для оценки значимости коэффициента корреляции, параметров уравнения регрессии и всего уравнения.

На основе данных таблицы построим уравнение регрессии: у_х=30,306--0,228х. Коэффициент регрессии а₁=-0,228 означает, что с повышением яловости на 1% среднегодовой удой на 1 корову уменьшается на 0,228 ц.

Коэффициент корреляции r=0,48, следовательно, связь между изучаемыми признаками в данной совокупности средней силы. Коэффициент детерминации r²=0,23 показывает, что 23% вариации результативного признака (среднегодовой удой на 1 корову) вызвано действием факторного признака (процента яловости).

В таблице критических точек распределения Фишера - Снедекора найдём критическое значение F-критерия при уровне значимости 0,05 и числе степеней свободы к₁=m-1=2-1=1 и k₂=n-m=30-2=28, оно равно 4,21. Так как рассчитанное значение критерия больше табличного (F=8,56>4,21), то уравнение регрессии признаётся значимым.

Для оценки значимости коэффициента корреляции рассчитаем t-критерий Стьюдента:

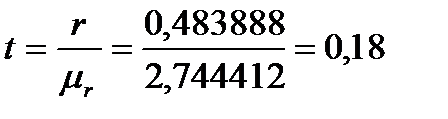
Таблица 3.4 - Корреляционно-регрессионный анализ взаимосвязи процента яловости и среднегодового удоя на 1корову

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,483888
R-квадрат	0,234147
Нормированный R-квадрат	0,206795
Стандартная ошибка	2,744412
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		64,47633	64,47633	8,560549	0,006743
Остаток		210,8903	7,531798
Итого		275,3667
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	30,30585	1,372702	22,07752	2,99E-19	27,494	33,11771	27,494	33,11771
Переменная X 1	-0,22754	0,077768	-2,92584	0,006743	-0,38684	-0,06824	-0,38684	-0,06824

В таблице критических точек распределения Стьюдента найдём критическое значение t-критерия при уровне значимости 0,05 и числе степеней свободы n-1=30-1=29, оно равно 2,0452. Так как расчётное значение меньше табличного, то коэффициент корреляции является незначимым.

ВАРИАНТЫ ЗАДАНИЙ

ВАРИАНТ №1	ВАРИАНТ №2
№ хозяйства	Качество почв, балл (х)	Урожайность оз. пшеницы, т/га (у)	№ хозяйства	Урожайность овощей с 1га, т (х)	Затраты труда на 1т, чел.-час (у)
		2,0
		3,0
		1,5
		1,5
		3,5
		3,5
		3,5
		2,5
		2,0
		2,0
		2,5
		2,5
		1,5
		2,0
		2,5
		3,5
		2,5
		3,5
		4,2
		3,0
		2,5
		2,5
		3,0
		4,2
		2,5
		3,0
		3,5
		4,0
		3,5
		2,0

ВАРИАНТ №3	ВАРИАНТ №4
№ хозяйства	Урожайность сахарной свёклы, ц/га (х)	Затраты труда на 1ц, чел-час (у)	№ хозяйства	Урожайность картофеля, ц/га (у)	Уд. вес сортовых посевов, %(х)
		1,8
		1,4
		1,4
		1,4
		1,6
		1,4
		1,3
		1,2
		1,6
		1,3
		1,5
		1,6
		1,5
		1,2
		1,5
		1,2
		1,1
		1,3
		1,3
		1,5
		1,4
		1,4
		1,4
		1,6
		1,1
		1,6
		1,7
		1,7
		1,5
		1,3

ВАРИАНТ №5	ВАРИАНТ №6
№ хозяйства	Качество почв, балл (х)	Урожайность картофеля, т/га (у)	№ хозяйства	Урожайность картофеля, т/га (у)	Удельный вес сортовых посевов, % (х)

ВАРИАНТ №7	ВАРИАНТ №8
№ хозяйства	Урожайность зерновых, ц/га (у)	Затраты труда на 1 га, чел.-час (х)	№ хозяйства	Бонитет почв, балл (х)	Урожайность овощей, ц/га (у)
		9,0
		14,0
		20,0
		19,6
		21,7
		6,4
		8,8
		14,2
		6,4
		8,7
		10,9
		12,6
		18,8
		10,9
		10,3
		19,4
		15,7
		14,0
		12,0
		8,7
		18,6
		21,3
		20,0
		11,7
		13,4
		15,2
		11,4
		17,9
		14,0
		19,6

ВАРИАНТ №9	ВАРИАНТ № 10
№хозяйства	Производственная площадь, тыс. м^2(х)	Выручка от реализации, млн. руб. (у)	№хозяйства	Живая масса коров, ц (х)	Среднегодовой удой от 1 коровы, ц (у)
	1,8			4,6	39,2
	1,7			4,6	43,3
	2,0			3,3	31,0
	1,6			5,6	50,0
	1,9			4,6	43,3
	1,4			5,1	48,4
	1,5			3,6	27,9
	1,9			4,6	39,2
	2,0			5,6	48,4
	2,0			4,1	34,8
	1,5			5,1	50,0
	1,6			4,6	34,8
	1,7			3,1	27,9
	1,9			3,6	31,0
	2,0			4,1	31,0
	1,4			5,6	27,9
	1,5			4,6	39,2
	1,9			4,1	34,8
	1,8			5,1	48,4
	1,8			5,1	43,3
	2,0			3,6	31,0
	1,4			4,1	31,0
	1,9			4,6	43,3
	2,0			5,0	48,4
	1,5			4,1	34,8
	1,5			5,1	50,0
	1,6			4,6	39,2
	1,9			4,1	34,8
	1,7			4,6	39,2
	1,4			4,1	39,2

ВАРИАНТ №11	ВАРИАНТ №12
№ хозяйства	Расход кормов на корову за год, ц.к.ед (х)	Удой на среднегодовую корову, ц (у)	№ хозяйства	Удой на среднегодовую корову, ц (у)	Процент яловости коров, % (х)
	44,8	34,5		34,5	13,5
	41,4	43,3		43,3	12,1
	47,3	40,0		40,0	15,1
	42,9	37,0		37,0	16,0
	47,3	40,0		40,0	18,0
	47,4	34,5		34,5	12,7
	49,3	38,9		38,9	14,1
	59,1	35,3		35,3	12,5
	54,2	34,5		34,5	14,1
	50,5	43,3		43,3	13,2
	59,1	40,0		40,0	17,2
	54,3	34,5		34,5	14,2
	58,9	40,0		40,0	13,3
	45,7	37,0		37,0	16,3
	50,8	35,3		35,3	14,2
	44,9	37,0		37,0	14,6
	51,3	38,9		38,9	15,1
	54,5	40,0		40,0	16,7
	52,7	43,3		43,3	14,1
	54,9	34,5		34,5	11,5
	60,1	35,3		35,3	15,9
	57,0	37,0		37,0	14,5
	41,4	40,0		40,0	11,9
	56,2	35,3		35,3	13,8
	55,0	34,5		34,5	12,5
	50,5	37,0		37,0	16,4
	59,9	43,3		43,3	11,1
	47,8	38,9		38,9	14,2
	57,4	40,0		40,0	11,0
	60,1	35,3		35,3	13,4

ВАРИАНТ № 13	ВАРИАНТ № 14
№ хозяйства	Урожайность зерновых с 1га, ц	Удельный вес сортовых посевов, %	№хозяйства	Посевная площадь, тыс. га (х)	Выручка от реализации, млн. руб. (у)
				5,4
				5,7
				5,1
				5,8
				6,0
				5,7
				6,1
				5,4
				5,8
				5,5
				4,7
				6,1
				6,5
				5,1
				5,4
				5,7
				5,5
				5,8
				5,4
				6,0
				5,7
				4,7
				5,4
				6,1
				5,5
				6,1
				5,7
				5,5
				4,8
				5,4

ВАРИАНТ №15	ВАРИАНТ №16
№ хозяйства	Затраты труда на 1ц молока, чел.-час. (у)	Продуктивность коров, ц (х)	№ хозяйства	Бонитет почв, балл (х)	Урожайность зерновых, ц/га (у)
	7,1			27,5	14,0
	6,8			25,5	14,0
	5,8			23,5	9,5
	7,1			22,0	13,0
	6,0			27,5	15,0
	5,2			22,0	6,2
	7,1			23,5	9,5
	6,8			23,5	9,5
	5,8			18,5	6,2
	7,6			23,5	14,0
	6,8			26,5	15,0
	5,8			18,5	9,5
	8,0			23,5	13,0
	6,8			25,5	15,0
	5,8			22,0	9,5
	8,0			20,0	9,5
	6,8			20,0	9,5
	7,1			22,5	9,5
	8,0			23,5	13,0
	6,8			17,5	13,0
	6,8			17,5	6,2
	5,8			20,0	6,2
	7,1			25,5	9,5
	6,0			18,5	13,0
	7,6			22,0	6,2
	6,8			20,0	13,0
	6,0			27,5	9,5
	6,8			29,0	20,0
	6,0			26,5	20,0
	7,1			22,0	15,0

Дата добавления: 2015-06-28