Показатели центра распределения

Рр

ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ

ПРИМЕР ЗАДАНИЯ

По данным варианта 53 выполите РГР пользуясь методическими указаниями приведенными в п. 1

Таблица 2.1..- Процент яловости и среднегодовой удой на 1 корову в сельскохозяйственных организациях района

№ хозяйства	% яловости х	Среднегодовой удой на 1 корову, ц у	№ хозяйства	% яловости х	Среднегодовой удой на 1 корову, ц у	№ хозяйства	% яловости х	Среднегодовой удой на 1 корову, ц у

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Саратовский государственный аграрный университет им. Н.И. Вавилова»     Кафедра экономической кибернетики     Расчетно-графическая работа по статистике     Выполнила: студентка 2 курса, Б-М-АПК 202 Иванова Е.С. Проверила: доцент, к.э.н. Романова И.В.     Саратов 2013      

Оглавление:

Глава 1. Построение и графическое изображение вариационных рядов.............................. 3

Глава 2.. Статистические характеристики рядов распределения........................................... 7

2.1. Показатели центра распределения...................................................................................... 7

2.2. Показатели колеблемости признака.................................................................................... 9

2.3. Показатели формы распределения.................................................................................... 10

2.4. Статистические оценки параметров распределения....................................................... 12

2.5. Проверка гипотезы о законе нормального распределения............................................. 16

Глава 3. Корреляционно-регрессионный анализ.................................................................... 18

3.1. Определение параметров уравнения регрессии и показателей тесноты корреляционной связи............................................................................................................................................................ 18

3.2. Оценка значимости уравнения регрессии и параметров тесноты связи...................... 23

Приложения................................................................................................................................ 26

ГЛАВА 1. ПОСТРОЕНИЕ И ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ВАРИАЦИОННЫХ РЯДОВ

Имеем статистическую совокупность из 30 сельскохозяйственный организаций, охарактеризованных двумя признаками: процентом яловости и среднегодовым удоем на 1 корову.

Таблица 3.1- Процент яловости и среднегодовой удой на 1 корову в сельскохозяйственных организациях района

№ хозяйства	% яловости х	Среднегодовой удой на 1 корову, ц у	№ хозяйства	% яловости х	Среднегодовой удой на 1 корову, ц у	№ хозяйства	% яловости х	Среднегодовой удой на 1 корову, ц у

Дискретный вариационный ряд следует построить по результативному (зависимому) признаку (обозначим его у), интервальный - по факторному (независимому) - х. Факторный – это признак, который оказывает влияние на связанный с ним результативный признак. Результативный – это признак, подвергающийся влиянию факторного, зависящий от него. В результате логического рассуждения приходим к выводу, что зависимым, результативным признаком в данном случае будет среднегодовой удой на 1 корову, независимым, факторным – процент яловости.

Для того чтобы составить дискретный вариационный ряд, необходимо расположить значения признака в порядке возрастания, т.е. произвести ранжирование статистических данных, а затем подсчитать частоты (сколько раз встречается то или иное значение признака).

Для графического изображения дискретного ряда служит многоугольник (полигон). При его построении на оси абсцисс откладываются варианты, на оси ординат - частоты.

Для построения интервального вариационного ряда:

· определяется число групп (число интервалов) по формуле Стерджесса:

K=1+3,32*lg(n), (1)

где К - число групп (интервалов); n - число единиц наблюдения;

· рассчитывается величина интервала, т.е. разность между верхним и нижним значением признака в группе:

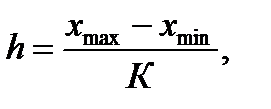(2)

где х_max – максимальное значение признака; x_min – минимальное значение признака;

· формируются группы, т.е. устанавливаются верхние и нижние границы для каждого интервала. Нижней границей для первой группы будет x_min (или эта величина, уменьшенная не более чем на половину величины интервала); чтобы найти верхнюю границу, нужно к нижней границе прибавить величину интервала h. Верхняя граница первой группы будет одновременно нижней границей для второго интервала. Чтобы найти верхнюю границу, к полученному значению опять прибавляют величину интервала и т.д.;

· подсчитывается число значений признака, попавших в каждый интервал; варианты, совпадающие с границами частичных интервалов, включаются в правый интервал.

Графически интервальный ряд изображают с помощью гистограммы. На оси абсцисс берутся отрезки, соответствующие величине интервала. На каждом отрезке строят прямоугольник, длина второй стороны которого соответствует частоте.

Таблица 3.2- Дискретный вариационный ряд распределения среднегодового удоя на 1 корову

Варианты	Частоты	Накопленные частоты

Варианты

Частоты

Ряд1

Рис. 1. Полигон распределения сельскохозяйственных предприятий по

Таблица 3.3 - Интервальный вариационный ряд распределения процента яловости

Интервалы	Частота	Накопленная частота	Середина интервала
9 – 14			11,5
14 – 19			16,5
19 – 24			21,5
24 – 29			26,5
29 – 34			31,5
34 – 39			36,5

11,5

16,5

21,5

26,5

31,5

36,5

%яловости

Частоты

Ряд1

Рис. 2. Гистограмма распределения сельскохозяйственных предприятий по проценту яловости

Глава 2. Статистические характеристики рядов распределения

Рис. 3.2. Показатели центра распределения

ГЛАВА 2. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ РЯДОВ РАСПРЕДЕЛЕНИЯ

К показателям центра распределения относятся средняя арифметическая, мода и медиана.

Под средней величиной понимают обобщающий показатель, характеризующий типичный уровень признака и рассчитанный на единицу однородной совокупности.

Средняя арифметическая вычисляется по формулам:

простая 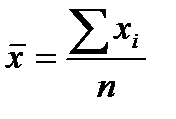; взвешенная ,

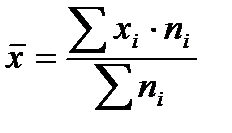где 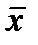- среднее значение признака; 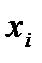- варианты; 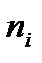- частоты; 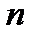- численность совокупности.

Мода- величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности.

В дискретных рядах распределения модой будет варианта с наибольшей частотой.

В интервальном ряду мода определя6ется по формуле:

,

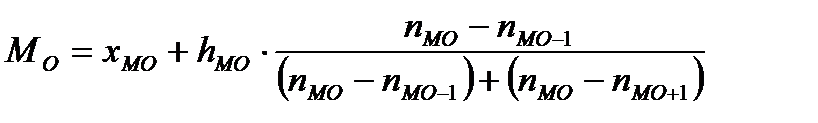где 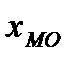- нижняя граница интервала, содержащего моду; 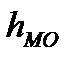- величина модального интервала; 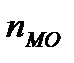- частота модального интервала; 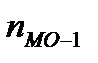- частота интервала, предшествующего модальному; 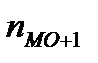- частота послемодального интервала.

Медианой называется варианта, расположенная в середине вариационного ряда.

Если ряд дискретный имеет нечётное число единиц, то медианой будет варианта, расположенная в середине упорядоченного ряда и её порядковый номер 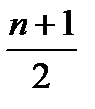. Если ряд состоит из чётного числа членов, то медианой будет средняя арифметическая из двух вариант с порядковыми номерам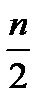и: и .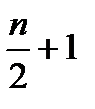

В интервальном ряду медиана рассчитывается по формуле:

где 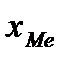- нижняя граница медианного интервала; 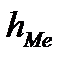- величина медианного интервала; - сумма накопленных частот, предшествующих медианному интервалу; 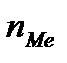-частота медианного интервала. Медианным является интервал, накопленная частота которого равна или больше полусуммы всех частот.

Дата добавления: 2015-06-28