Пример выполнения расчетно-проектировочной работы 2 страница

Рис.7. К определению М_К2 на втором участке.

На втором участке координата z₂ изменяется в пределах 0 £ Z₂ £ 2 l. Уравнение равновесия для отсечённой части вала записывается в виде

, .

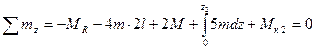Крутящий момент на границах участка принимает значения:

при z₂=0 М_К2= 2M=200Н×м, при z₂= 2 l M_К2= -8М=-800Н×м.

3.3 Третий участок (рис.8)

6M M_K3

2M

4m 5m

z

M_R 2l 2l z₃

Рис.8. К определению М_К3 на третьем участке.

Координата z₃ для третьего участка изменяется в пределах 0 £ Z₃ £ l. Уравнение равновесия отсечённой части вала и значения крутящего момента в граничных сечениях участка соответственно равны:

Sm_z= -M_R-4m×2 l +2M+5m×2 l -6M+M_К3= 0, М_К3= -2М=-200Н×м.

На третьем участке крутящий момент постоянен по длине участка и равен М_К3= -2М=-200Н×м.

3.4 Четвёртый участок (рис.9).

На четвёртом участке координата z₄ изменяется в пределах 0 £ Z₄ £ l. Уравнение равновесия для отсечённой части вала записывается в виде

Sm_z= -M_R-4m×2 l +2m+5m×2 l -6M+4M+M_К4= 0, М_К4= -6М=-600Н×м.

На четвёртом участке крутящий момент постоянен по длине участка и равен М_К4= -6М=-600Н×м.

6M 4M M_K4

2M

4m 5m

z

M_R

2l 2l l z₄

Рис.9. К определению М_К4 на четвёртом участке.

3.5 Пятый участок (рис.10)

6M 4M 10M

2M M_K5

4m 5m 2m

z

M_R

2l 2l l l z₅

Рис. 10. К определению М_К5 на пятом участке.

Координата z₅ на пятом участке изменяется в пределах 0 £ Z₅ £ 2 l. Уравнение равновесия для отсечённой части вала имеет вид

Sm_z = -M_R-4m×2 l -2m-5m×2 l -6M+4M-10M- M_К5= 0;

M_К5= 4М+2mZ₅.

Крутящий момент на границах пятого участка принимает значения:

при z₅=0 M_К5= 4M=400Н×м; при z₅= 2 l M_К5= 8М=800Н×м.

По результатам вычислений строится эпюра крутящих моментов М_К (рис.5, б)

4. Определение закона изменения касательного напряжения по участкам вала.

Для определения касательного напряжения по участкам вала предварительно вычисляются полярные моменты сопротивления сечений:

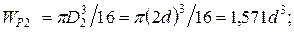
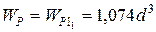Затем наименьшее значение полярного момента сопротивления (в данном примере ) принимается за и определяются значения полярных моментов сопротивления поперечных сечений вала пропорционально ; ; ; ; .

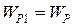4.1 На первом участке закон изменения касательного напряжения в соответствии с формулой (3) имеет вид:

.

Касательное напряжение линейно зависит от координаты Z₁ и на границах участка принимает значения:

при z₁= 0 ; при z₁= 2 l .

4.2 На втором участке касательное напряжение на границах участка принимает значения:

;

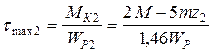при z₂ = 0 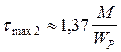; при z₂ = 2 l .

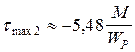4.3 На третьем участке касательное напряжение равно:

.

4.4 Касательное напряжение на четвертом участке равно:

.

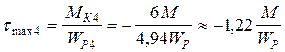4.5 На пятом участке касательное напряжение линейно зависит от координаты z₅ и на границах участка принимает значения:

;

при z₅ = 0 ; при z₅= 2 l .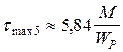

По результатам вычислений строится эпюра касательных напряжений t_max (рис.5.в).

5. Определение размеров поперечных сечений вала из условия проч-ности.

Опасным является сечение, в котором действует наибольшее максимальное касательное напряжение.

Следовательно условие прочности запишется: max 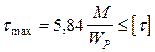. Из условия прочности определяется диаметр вала в опасном сечении:

.

6. Определение размеров поперечных сечений вала из условия

жесткости. Условие жесткости записывается для сечения, где действует наибольший крутящий момент (рис. 5,б), при наименьших соотношениях размеров поперечного сечения вала. Для рассматриваемого примера усло­вие жесткости записывается для крайнего правого сечения вала (на 5 уча­стке).

где ,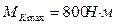

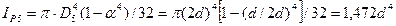
Из условия жесткости определяется диаметр вала:

Анализируя значения диаметра вала, полученные из условия прочно­сти и условия жесткости, окончательно принимаем 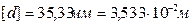. Соответственно, размеры сечений вала по участ­кам равны: ; ; ;

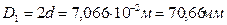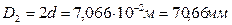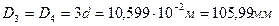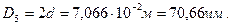
7. Определение закона изменения углов закручивания на участках вала.

Для определения углов закручивания по участкам вала пред-варительно вычисляются полярные моменты инерции сечений:

I_P1= pD₁⁴(1-a⁴)/32 = p(2d)⁴[1-(1,5d/2d)⁴]/32= 1,074d⁴;

I_P2= pD₂⁴/32 = p(2d)⁴/32 = 1,571d⁴;

I_P3=pD₃⁴/32 = p(3d)⁴/32 = 7,951d⁴;

I_P4=pD₄⁴/32 = p(3d)⁴/32 = 7,951d⁴;

I_P5= pD₅⁴(1-a⁴)/32 = p(2d)⁴[1-(d/2d)⁴]/32 = 1,472d⁴.

7.1 На первом участке угол закручивания в соответствии с законом Р.Гука равен:

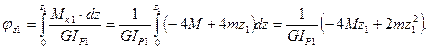
Угол закручивания изменяется по кривой второго порядка и на границах участка принимает значения

при z₁= 0 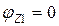, при z₁= 2 l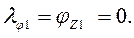

Определим выпуклость кривой , следовательно кривая 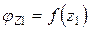выпукла вниз.

Условие экстремума кривой ,

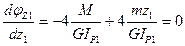, следовательно функция 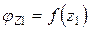имеет экстремум при z₁ = l.

Вычислим угол закручивания

при z₁ = l

7.2 На втором участке угол закручивания изменяется по кривой

второго порядка

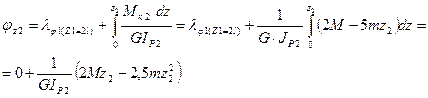
Угол закручивания на границах второго участка принимает значения

при z₂=0 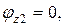при z₂=2 l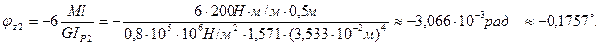

Определим выпуклость кривой 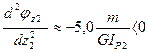. Следовательно кривая выпукла вверх.

Условия экстремума кривой

.

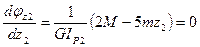Следовательно функция имеет экстремум при z₂=0,4 l. Вычислим угол закручивания при z₂=0,4 l

7.3 На третьем участке угол закручивания равен:

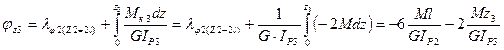
при z₃=0 ,

при z₃= l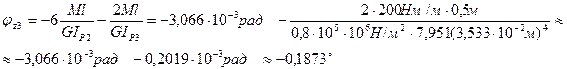

7.4 Угол закручивания на четвертом участке равен:

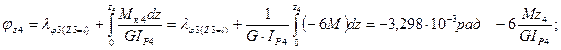
при z₄=0 ,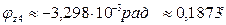

при z₄= l

7.5 На пятом участке угол закручивания изменяется по кривой

второго порядка:

Угол закручивания на границах пятого участка принимает значения

при z₅=0 ;

при z₅=2 l

Определим выпуклость кривой 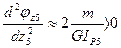. Следовательно кривая выпукла вниз. Условие экстремума кривой:

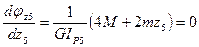, . Следовательно функция имеет экстремум за пределами (z₅ = -2 l) пятого участка. По результатам вычислений строится эпюра углов закручивания j по длине вала (рис. 5, г).

8. В классе ПЭВМ кафедры студент реализует машинный вариант выполнения РПР, сопоставляет результаты традиционного и машинного расчетов.

Вопросы и задания для самопроверки.

1. При каком нагружении брус испытывает деформацию кручения?

2. Что называется валом?

3. Какое правило знаков принято для крутящих моментов?

4. Какие напряжения возникают в поперечных сечениях вала круглого сечения при кручении? Закон его распределения по высоте сечения вала?

5. Как записывается условие прочности при кручении?

6. Напишите выражения полярных моментов инерции и полярных момен-тов сопротивления круглого (сплошного и кольцевого) сечения.

7. Как выбираются допускаемые напряжения при кручении?

8. Как записываются условия жесткости при кручении?

9. Что называется жесткостью сечения вала?

10. Приведите примеры реальных конструкций, работающих в условиях кручения, применительно к вашей специальности.

Дата добавления: 2015-06-29