Поперечные силы и изгибающие моменты

III.ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ

ОСНОВНЫЕ ПОЛОЖЕНИЯ И ОПРЕДЕЛЕНИЯ

Деформацию бруса, в поперечных сечениях которого, под воздействием внешних нагрузок, возникают внутренние силовые факторы - изгибающие моменты (М_х, М_у) и поперечные (перерезывающие) силы (Q_y, Q_x) - назы­вают поперечным изгибом. Если в сечении поперечные силы (Q_y, Q_x) от­сутствуют, то изгиб называют чистым.

В настоящем методическом пособии рассматривается брус с прямоли­нейной осью, сечение которого имеет хотя бы одну ось симметрии, а плос­кость действия внешних нагрузок совпадает с плоскостью симметрии. Ис­кривленная ось бруса - плоская кривая, лежащая в плоскости действия внешних нагрузок. Такой изгиб называют поперечным прямым изгибом. Брусья, испытывающие прямой изгиб, принято называть балками.

Балка при изгибе деформируется таким образом, что часть волокон (слоев) испытывает растяжение, а часть - сжатие. В выпуклой части во­локна (слои) растянуты, а в вогнутой - сжатые. Деформация волокон не­прерывно изменяется по высоте сечения, следовательно существует слой, который не деформируется и напряжения в нем равны нулю. Такой слой называется нейтральным. Пересечение нейтрального слоя балки с попе­речным сечением образует нейтральную линию (нейтральную ось).

Для оценки степени воздействия внешних нагрузок на брус необходимо определить внутренние силы (внутренние силовые факторы), которые про­тиводействуют стремлению внешних нагрузок деформировать брус. Зна­чение этих внутренних силовых факторов используют для оценки прочно­сти и жесткости балки. Для определения внутренних силовых факторов используют метод сечений.

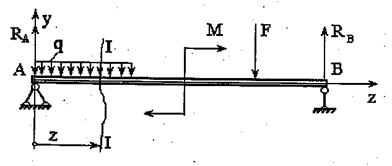
а)

б) в)

Рис. 1 Схема нагружения балки внешними нагрузками (а), и выявление возникающих внутренних силовых факторов (б, в).

Рассекаем балку сечением I - I (с абсциссой z) отбросив правую часть (рис. 1, в). В проведенном поперечном сечении (рис. 1, б) возникает два внутренних силовых фактора - поперечная (перерезывающая) сила Q_y и изгибающий момент М_х, заменяющие действие отброшенной части балки на оставленную. В том же сечении, но принадлежащем отброшенной части (рис. 1, в) возникают такие же по значению, но противоположно направ­ленные поперечная сила Q_y и изгибающий момент М_х. Правая и левая час­ти балки должны находиться в равновесии, поскольку вся балка находится в равновесии.

Внешние и внутренняя силы, приложенные к оставленной (левой) части бруса, образуют плоскую систему параллельных сил, к которым можно применять три уравнения статики: ,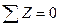

где R_q=qz - грузовая площадь распределенной нагрузки.

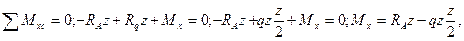
где R_q z=qz²/2 – момент грузовой площади.

Анализируя вышеприведенные выражения Q_y и М_х можно сделать сле­дующие выводы:

- поперечная сила Q_y численно равна алгебраической сумме внеш­них сил, находящихся по одну сторону от сечения;

- изгибающий момент М_х в сечении численно равен алгебраической сумме моментов от всех внешних сил, находящихся по одну сторо­ну от сечения, относительно центра тяжести этого сечения.

Для наглядного представления о характере изменения внутренних си­ловых факторов Q_y и М_х по длине балки строятся эпюры (графики) попе­речной силы Q_y и изгибающего момента М_х. По эпюрам Q_y и М_х опреде­ляются сечения, в которых действуют наибольшие значения этих величин, которые затем используются для расчетов на прочность и жесткость балки.

Для определённости при построении указанных эпюр устанавливаются правила знаков для Q_y и М_х. Представим отсеченную часть балки защем­ленной в проведенном сечении (рис. 2, а). Изгибающий момент в сече­нии считается положительным, если момент от внешних сил будет изги­бать балку выпуклостью вниз и отрицательным - выпуклостью вверх (рис. 2, а).

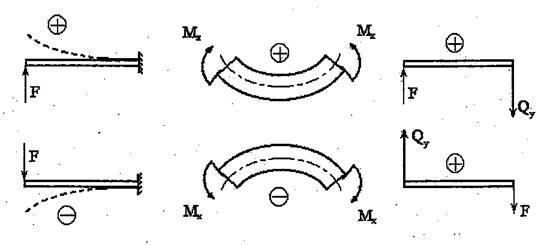
а) б)

Рис. 2. К определению правила знаков для Q_y и М_х.

Перерезывающая сила Q_y считается положительной, если внешняя сила стремится повернуть оставшуюся часть бруса относительно центра тяже­сти сечения по часовой стрелке (рис 2, б).

Поперечные силы и изгибающие моменты при заданной внешней на­грузке являются функциями абсцисс поперечных сечений Q_y=f(F, z) и M_x=f(F·z, z). Между Q_y, M_x и интенсивностью нагрузки q существуют диф­ференциальные зависимости, приведенные ниже, из которых вытекает ряд правил, используемых при построении и контроле правильности построе­ния эпюр Q_y и М_х:

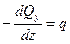- производная от перерезывающей силы Q_yпо абсциссе сече-

ния z, равна интенсивности нагрузки qв этом сечении;

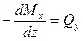- производная от изгибающего момента М_х по абсциссе сече-

ния z₃ равна перерезывающей силе Q_y в этом сечении;

- вторая производная от изгибающего момента М_х по абсциссеz, равна интенсивности нагрузки q в этом сечении.

ПРАВИЛА КОНТРОЛЯ ПОСТРОЕНИЯ ЭПЮР М_х И Q_y

1. На участке балки, где действует распределенная нагрузка q эпюра Q_y -наклонная прямая:

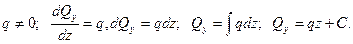
Эпюра изгибающих моментов М_х на этом участке - кривая второго по­рядка:

2. На участке балки отсутствует распределенная нагрузка q=0.

, следовательно Q_y=const - эпюра Q_yпараллельна оси абсцисс z.

Эпюра М_х – наклонная кривая;

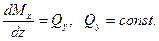
3. На участке, где Q_y положительна, момент М_х на эпюре возрастает > 0; если Q_y на участке балки отрицательна, то M_x убывает .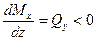

4. Если на участке, где , сила Q_y изменяясь по линейному закону, про­ходит через нулевое значение, то в соответствующем сечении изги­бающий момент М_х имеет экстремальное (максимальное или минимальное) значение .

5. В сечении, где приложена внешняя сосредоточенная сила на эпюре Q_y имеет место «скачок» на величину этой силы.

6. В сечении, где приложен внешний сосредоточенный изгибающий мо­мент на эпюре М_х имеет место «скачок» на величину этого момента.
Примеры построения эпюр поперечных (перерезывающих) сил Q_y и из­гибающих моментов М_х подробно рассмотрены ниже.

Дата добавления: 2015-06-29