Анализ систем автоматического управления

По литературе изучите корневые условия устойчивости линейных автоматических систем. Разберитесь, почему устойчивость системы определяют левой частью ДУ. Изучите влияние транспортного запаздывания на устойчивость системы. Научитесь пользоваться алгебраическими и частотными критериями устойчивости, а также их математическим определением с помощью компьютерных программ. Изучите методы выделения областей устойчивости. Нужно понять, что требования, предъявляемые к работе систем управления теми или иными ТП, могут быть различными. Нередко основным показателем качества является статическая погрешность, равная отклонению управляемой величины в новом положении равновесия от ее значения в исходном состоянии равновесия. Еще чаще принимают максимальные отклонения регулируемых величин и различные показатели демпфирования (затухания) процессов регулирования. Для сравнения качества регулирования на основе этих показателей используют соответствующие оценки, базирующиеся на конфигурации переходной функции. То есть реакции системы на ступенчатое воздействие. Ступенчатое воздействие широко распространено как типовое по следующим причинам:

· при отсутствии данных о действительном характере возмущающих воздействий в системе предполагается, что, ограничив максимум реакции систем на ступенчатое возмущение, можно гарантировать это ограничение наибольшего отклонения регулируемой величины при другом возмущении;

· критерии качества, определяемые реакцией системы на ступенчатое воздействие (степень затухания, динамическая погрешность, время регулирования и другие) наглядны, просты, их зависимость от настройки регулятора легко поддается истолкованию;

· параметры настройки, установленные на основании реакции системы на ступенчатое воздействие, дают приемлемые, хотя и не вполне экономичные результаты в реальных условиях работы даже сравнительно простых систем.

Вместе с тем необходимо знать, что реакция системы на ступенчатое воздействие не всегда может служить достоверным критерием качества при воздействиях другого вида. Часто важнейшей экономической целью управления ТП является минимум материальных, энергетических и других потерь, обусловленных отклонениями хода ТП от оптимального. В этом заключается основная особенность управления энергоемкими объектами.

Действительно, при автоматизации тех или иных ТП часто встречают случаи, когда между управляемой величиной х и каким-либо сводным технико-экономическим показателем Э, среднее значение которого надо поддерживать минимальным или максимальным, существует четко выраженная экстремальная зависимость Э=f(х). В частности, такая зависимость имеет место между потерями зерна и высотой среза жатки комбайна, экономической эффективностью тепличных, животноводческих, птицеводческих комплексов и технологическими параметрами микроклимата в них.

Разлагая зависимость Э=f(х) в ряд Маклорена по степеням 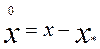для средних за время эксплуатации Т экономических потерь ΔЭ_Т, получим:

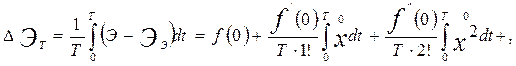(28)

где Э _э - экстремальное значение Э, соответствующее нулевому отклонению управляемой величины х от заданной х_*; t – текущее время.

Ввиду экстремальной зависимости Э=f(х) производная f’(0)=0. В силу равновероятности отклонения х от задания в ту или иную стороны средние по времени значения нечетных степеней 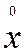практически равны нулю. Вследствие малых отклонений управляемой величины от заданной средними по времени значениями высших степеней 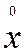можно пренебречь. Следовательно, с учетом очевидного равенства f(0)=0 справедливо выражение:

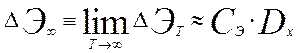, (29)

где – 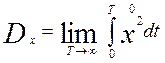дисперсия стационарного случайного процесса изменения 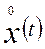; 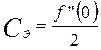- коэффициент пропорциональности, не зависящий от управляемой величины х.

Таким образом, минимуму величины ΔЭ_∞ отвечает минимум D_x и выбор дисперсии процесса отклонения управляемой величины от заданной в качестве основного показателя (критерия) управления определяется предварительным технико-экономическим обоснованием. Важно усвоить его основные моменты.

Следует также познакомиться с параметрической чувствительностью, запасом устойчивости и их оценками (корневыми, частотными и др.). Эти оценки широко используют в качестве ограничений области, в которой осуществляют оптимизацию параметров системы по основному (технически или экономически обоснованному) показателю качества управления.

Повышение качества работы системы на основе минимизации дисперсии управляемой величины обычно достигается установкой значений настроечных параметров регулятора, обеспечивающих максимизацию свободного члена в соответствующем характеристическом уравнении. Эта максимизация осуществляется при ограничении колебательности системы путем использования тех или иных оценок затухания переходных процессов.

Методические рекомендации по выполнению раздела

Выполнение данного раздела состоит из трех задач:

· Задача 1. Опишите Ваш ТП структурной схемой.

· Задача 2. Определите устойчивость работы Вашей ЭП установки при заданных параметрах.

· Задача 3. Рассчитайте параметры настройки регулятора для Вашей системы автоматического управления ТП.

Дата добавления: 2015-06-29