Объекты автоматического управления

Прежде всего, следует уяснить, что в общем случае влияние внешнего воздействия на управляемую величину объекта описывают с помощью дифференциального уравнения (ДУ). Если это уравнение нулевого порядка, то есть алгебраическое, то соответствующий объект управления (ОУ) называют статическим или безинерционным. ОУ, описываемые ДУ более высокого порядка, называют динамическими. Приравнивая нулю все производные по времени t в обеих частях ДУ, получают алгебраическое уравнение, связывающее входную (внешнюю) и выходную (управляемую) величины объекта в установившемся режиме. Зависимость определяемая указанным алгебраическим уравнением называют статической характеристикой объекта.

ОУ называют линейным, если его выходные x(t) и входные y(t) воздействия связаны линейным ДУ. Дифференциальное уравнение n -го порядка
называют линейным, если все его коэффициенты а₀, а₁, а_n не зависят от управляемой величины х, то есть они могут быть функциями независимой переменной t или постоянными величинами. Нелинейные ОУ описывают нелинейными ДУ или нелинейными алгебраическими уравнениями. В частности, большинство реле относят к классу нелинейных статических элементов, поскольку их описывают нелинейными алгебраическими уравнениями. ОУ, коэффициенты дифференциальных или алгебраических уравнений, которые не меняются во времени, называют стационарными. В противном случае ОУ называют нестационарными.

Реакцию объекта на скачкообразное входное воздействие при величине скачка, равному единице, называют переходной функцией. Если переходная функция является ограниченной, то говорят, что объект обладает свойством самовыравнивания (саморегулирования). Реакцию объекта на единичное импульсное воздействие называют весовой функцией или импульсной характеристикой. Производная по времени от переходной функции совпадает с импульсной характеристикой. Переходные и весовые функции относят к классу временных характеристик объекта.

Изображение Лапласа весовой функции называют передаточной функцией (ПФ) объекта W(s), которую можно представить в следующем виде:

, (26)

где X(s) и Y(s) – изображения Лапласа сигналов x(i) и y(t) соответственно, 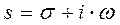– комплексная переменная. При σ=0, то есть 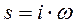ПФ обращается в комплексную частотную характеристику (КЧХ) объекта.

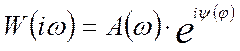, (27)

где А(ω) – амплитудно-частотная характеристика (АЧХ), отражающая изменения амплитуд, проходящих через объект гармонических сигналов, в зависимости от частоты ω; ψ(ω) – фазо-частотная характеристика (ФЧХ), отражающая фазовый сдвиг между входными и выходными гармоническими сигналами объекта как функцию частоты ω. Временные и частотные характеристики объекта называют динамическими.

Помимо самовыравнивания для многих ОУ в автоматизированном электроприводе характерны и другие свойства: значительные запаздывания, высокие аккумулирующие способности. Эти свойства существенно влияют на надежность и качество управления соответствующим ТП, а также на выбор автоматического УУ.

Дата добавления: 2015-06-29