Бинарные отношения. Пусть А и В – два произвольных множества

Пусть А и В – два произвольных множества.

Определение. Бинарным отношением 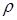из множества А в множество В называется всякое подмножество прямого произведения 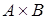; если А=В, то говорят о бинарном отношении на множестве А. Обозначение: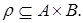

Тогда 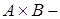это универсум U.

Пример. 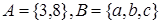. Положим

.

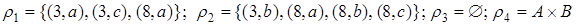Используют две формы записи принадлежности некоторой упорядоченной пары заданному бинарному отношению 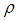– инфиксную и префиксную. Инфиксная форма записи: 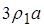; префиксная форма записи: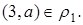

Приведем еще несколько примеров бинарных отношений.

Пример 1. На множестве N натуральных чисел определим бинарное отношение 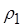так: .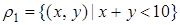

Тогда (1, 1) 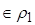, (5, 4) 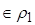, но (6, 7) .

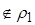Пример 2. На множестве R вещественных чисел определим бинарное отношение < (меньше) по правилу < = {(x, y)| x < y }.

Тогда (2,1; 3) Î <, (5, 8) Î <; но (1, 1) Ï < (неверно, что 1<1), (8, 5) Ï < (неверно, что 8<5).

Пример 3. На множестве людей определим бинарное отношение 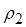(брат) по правилу 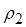={(a, b)| a является братом b }.

Тогда, если Иван – брат Анны, то (Иван, Анна)Î 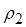, но (Анна, Иван)Ï.

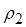Пример 4. Пусть 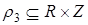определяется так

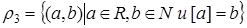([ a ] – знак целой части числа а).

Тогда (5,3; 5) Î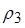, (6, 6) Î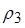, но (2,1; 4) Ï.

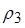Пример 5. Пусть 2 ^M – булеан некоторого множества M. На булеане 2 ^M определим бинарное отношение Í (отношение включения) по правилу

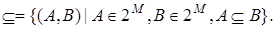
По аналогии с бинарным отношением вводится понятие п – арного отношения, как подмножества прямого произведения п множеств, .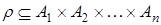

Определение Множество точек плоскости, координаты (x, y) которых образуют упорядоченные пары некоторого бинарного отношения 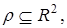называется графиком бинарного отношения.

Пусть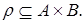

Определение. Областью определения 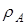бинарного отношения 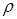называется множество всех первых элементов упорядоченных пар отношения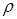

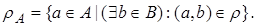
Определение. Областью значений 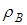бинарного отношения 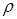называется множество всех вторых элементов упорядоченных пар отношения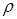

.

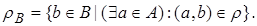
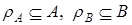Определение. Отношением 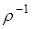, обратным к отношению 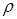, называют подмножество прямого произведения 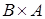, такое, что .

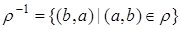Определение. Дополнением 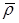отношения 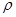называют бинарное отношение, определяемое как множество всех упорядоченных пар, не входящих в ,

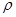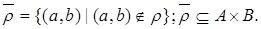
Пример. Пусть 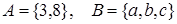, 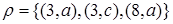. Тогда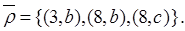

Определение. Тождественным отношением I называют подмножество А ² такое, что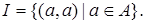

Пример. 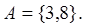Тогда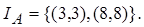

Пусть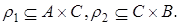

Определение. Композицией 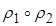отношени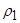й и 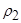называют бинарное отношение из множества А в множество В, определяемое так

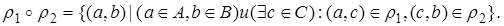
Итак, всякая упорядоченная пара 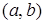из отношения 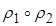образовалась благодаря существованию хотя бы одного элемента 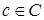такого, что он образует упорядоченную пару как с элементом 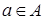(второй элемент пары из множества 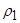), так и с элементом 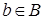(первый элемент пары из множества ).

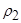Пусть 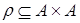, композиция 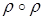обозначается иначе чер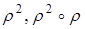ез через 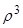и так далее.

Пример. Пусть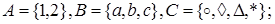

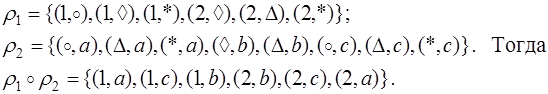
Утверждение. Пусть 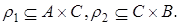Тогда

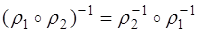
Дата добавления: 2014-01-03